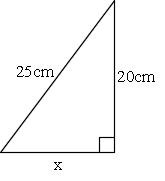
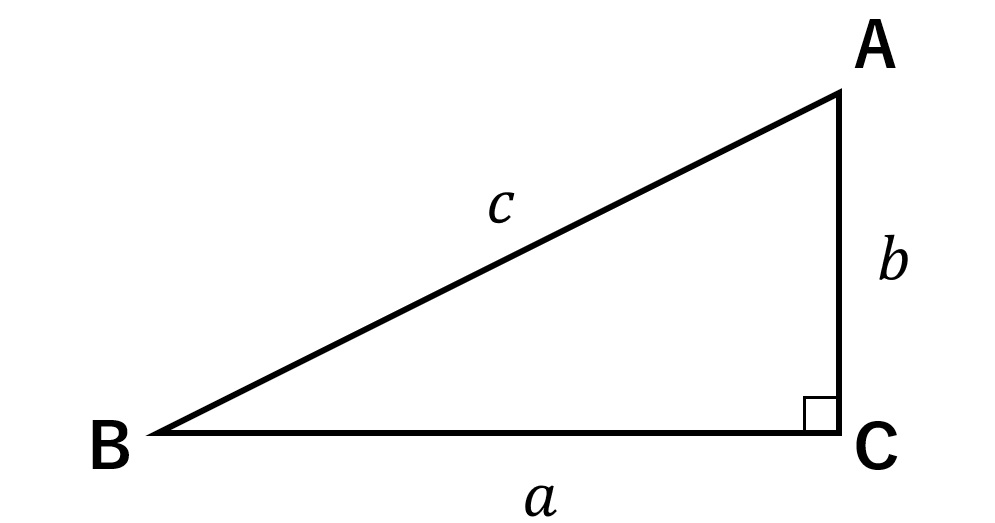
应用勾股定理:斜边平方=两直角边平方之和 例如,对于任意一直角三角形而言,设两直角边长度分别为a和b,斜边长为c,则根据勾股定理可得到公式:a²b²=c² 对于题中的直角三角形来说,利用勾股定理可得:斜边=√(236²12²)=√≈2648 扩展资料: 中国古代称直角三角形为勾股形,并且直角次のような直角三角形の3辺の長さについては, a 2 b 2 =c 2 が成り立ちます.(これを 三平方の定理 といいます.) 直角三角形的角平分线定理 文/周国旗 直角三角形的角平分线到角两边的距离相等。直角三角形三条角平分线的交点叫内心,即内切圆的圆心。

三平方の定理 直角三角形の辺の長さを計算する4つの問題の解き方 Qikeru 学びを楽しくわかりやすく
三 平方 の 定理 直角 三角形
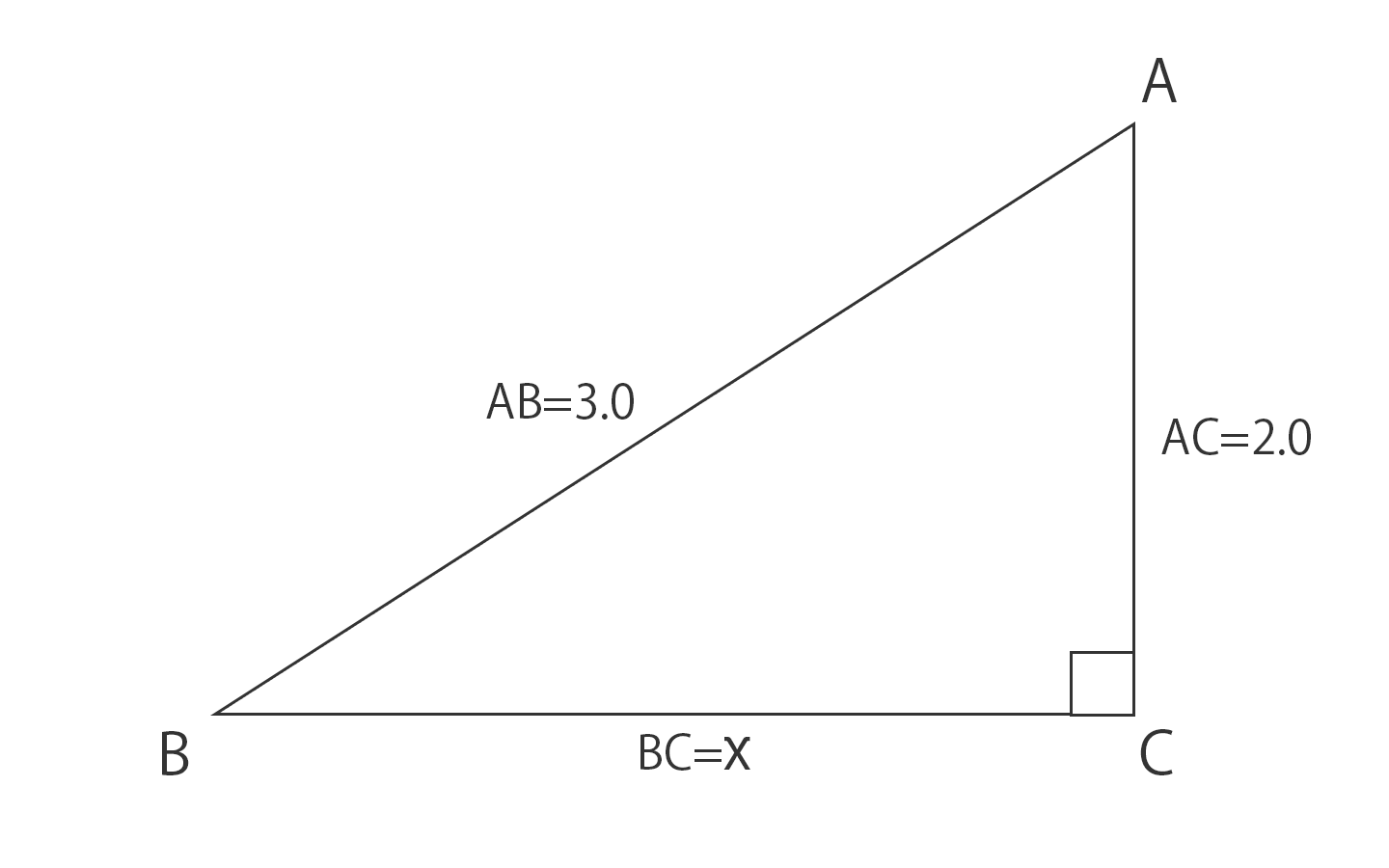
三 平方 の 定理 直角 三角形-已知一个直角三角形的三边的平方和为1800cm2,则斜边长为A30 cmB80 cmC90 cmD1 cm – 新东方在线网络课堂 题目 题型: 单选题 难度: 简单 来源:新东方在线网络课堂三平方の定理で直角三角形の辺の長さを計算してみると、 x² = 3² 5² x = √34 になるね。 答えが整数じゃなくてスッキリしないけど、こういう答えもありだ。 Step3 ピタゴラスが悩んだ直角二等辺三角形 つぎは、 直角二等辺三角形の辺の長さ を三平方の定理で計算する問題。 3平方の定理の逆




中3数学 三平方の定理 で最も重要なポイントとは 映像授業のtry It トライイット
三平方の定理を使って直角三角形の辺の長さを求める4つの問題 三平方の定理をつかった問題でよく出てくるのは、 直角三角形の辺の長さを求める問題。 今日はこの問題を4つのパターンに分けてみたぞ。 超基本タイプ; Excel 三角形の斜辺の長さ 高さ 底辺の長さを残りの2辺からする方法 まとめ三平方の定理ピタゴラスの定理を使えば直角三角形の辺の長さは大体わかる 三平方の定理で直角三角形の辺の長さを求める問題はどうだった 今日勉強した問題のパターンは4つだったな 超基本タイプ 三 平方 の 定理 直角 三角形 三 平方 の 定理 直角 三角形45°:45°:90°の直角三角形 こちらは直角以外の2角が2つとも45°になっている三角形、すなわち直角二等辺三角形です。 これは辺の比が1:1:√2になります。
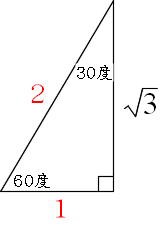
左の直角三角形が正三角形を半分にしたものです。 \(3\) 辺の比は暗記で、\(21\sqrt{3}\) です。 次に、右の直角三角形に三平方の定理を使うと、 最後の \(1\) 辺の長さが求まります。 最後の \(1\) 辺の長さを \(y\) とすると \(y^28^2=10^2\) \(y^264=100\) \(y^2=36\) \(y=±\sqrt{36}\)三平方の定理ともいう。 直角三角形において,直角である頂角の対辺の長さの平方は,他の2辺の平方の和に等しいという定理。 いま三角形 ABC において,∠C=∠R (直角) ,各頂角の対辺の長さをそれぞれ a,b,c とすれば a 2 +b 2 =c 2 である。 ピタゴラスの定理はその逆も成り立つ。3つの数 ,, が = を満たすとき、この3数を辺の長さとする三角形は直角三角形である。 これにより、たとえば辺の長さが 3,4,5 の三角形は直角三角形となる。 なぜなら、 = だからである。
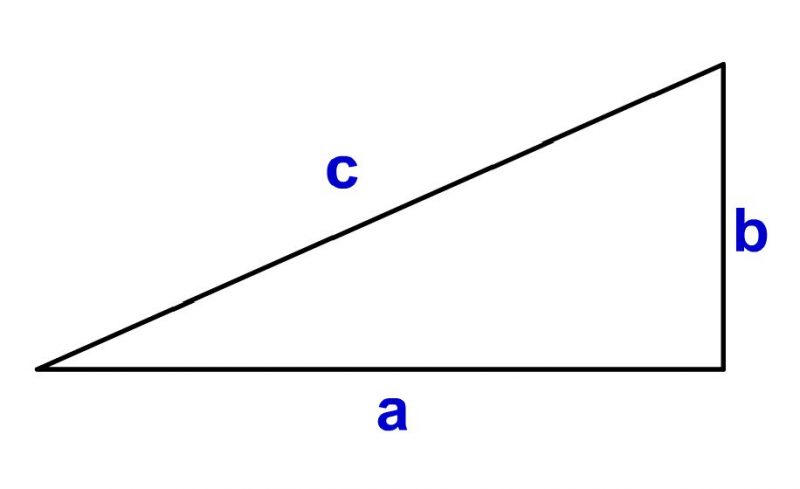
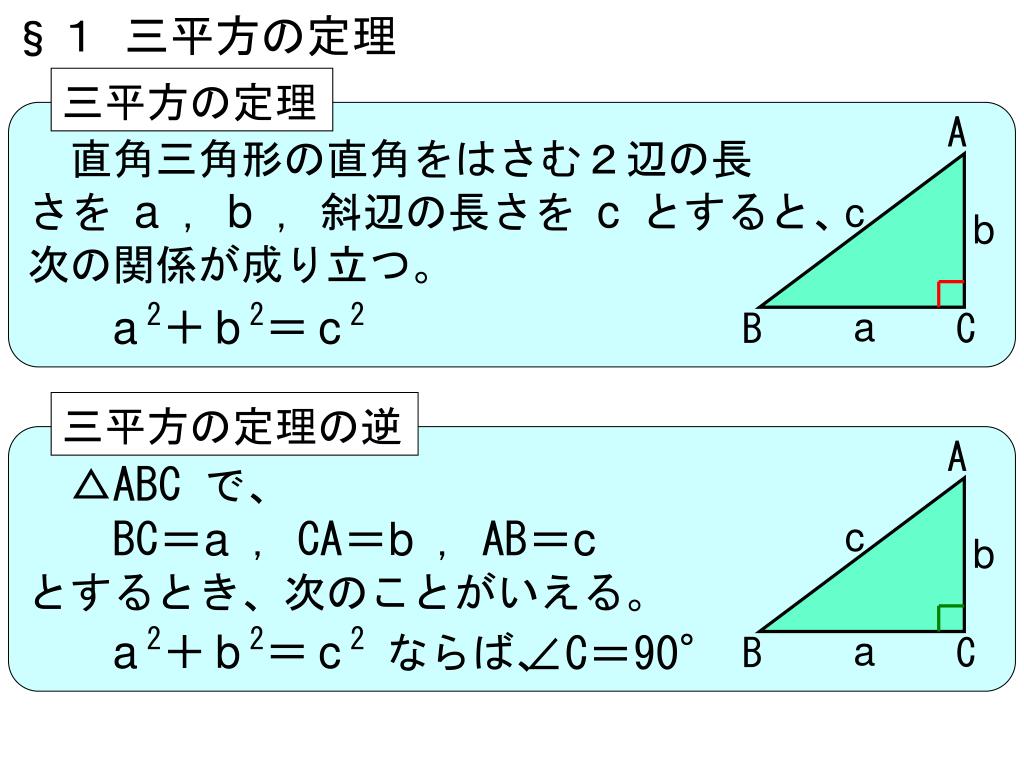
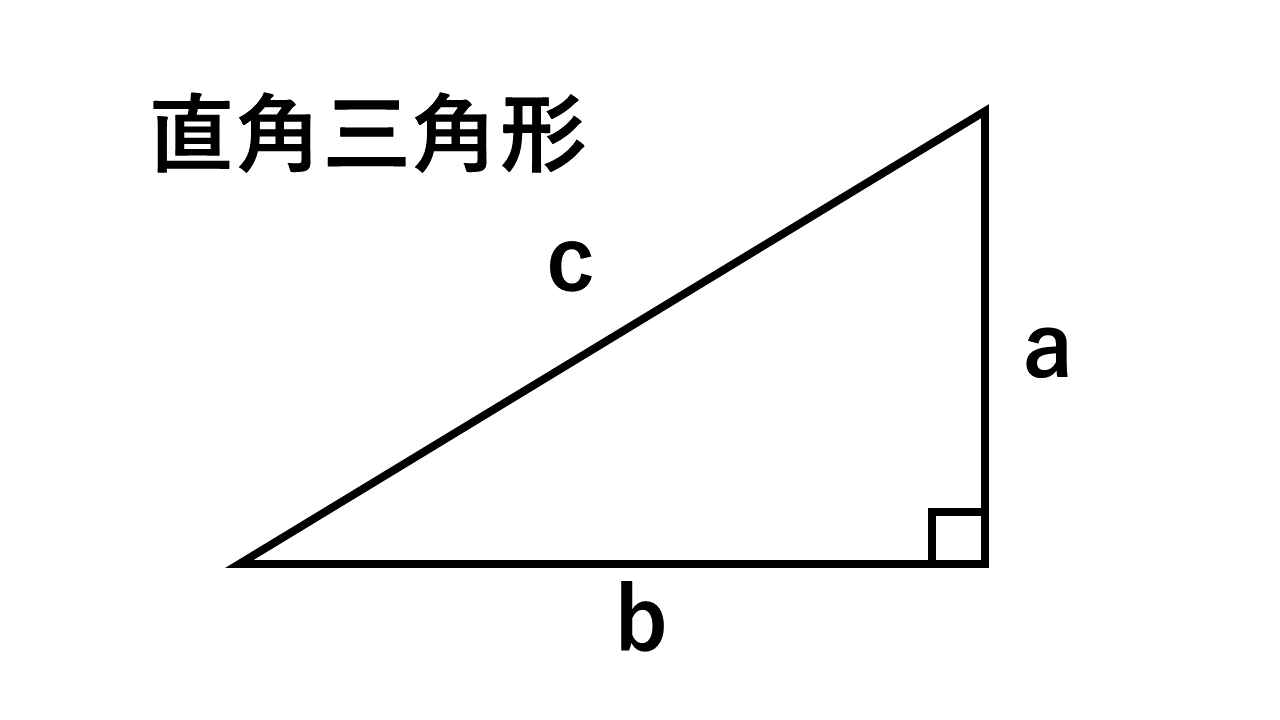
三平方の定理 とは、 直角三角形の直角をはさむ2辺の長さを a, b, 斜辺の長さを c としたときに、 公式 a2 b2 = c2 が成り立つ という定理です。 1、勾股定理 直角三角形的两条直角边的平方和等于斜边的平方。也叫毕达哥拉斯定理。表达式为a b =c 。 勾股定理 2、射影定理 在直角三角形中,斜边上的高是两条直角边在斜边射影的比例中项,每一条直角边又是这条直角边在斜边上的射影和斜边的比例中项。也叫欧几里德定理。三平方の定理 (さんへいほうのていり)、 勾股弦の定理 (こうこげんのていり)とも呼ばれる。 ピタゴラスの定理によって、直角三角形をなす3辺の内、2辺の長さを知ることができれば、残りの1辺の長さを知ることができる。




30 60 90 と 45 45 90 の直角三角形の辺の比 具体例で学ぶ数学



1
三平方の定理とは、直角三角形において 斜辺の長さの2乗は、他の辺の長さの2乗の和に等しくなる。 というものです。 文章だけでは、難しく見えますが 非常に単純な定理です。 このように 斜辺の2乗の数と 他の辺を2乗して足した数が等しくなるの下列定理有逆定理的是( )全等三角形的面积相等对顶角相等同角的余角相等直角三角形两条直角边的平方和等于斜边的平方 1年前 5个回答 直角三角形三边关系性质1:直角三角形两直角边的平方和等于斜边的平方性质2:在直角三角形中,两个锐角互余性质3:在直角直角三角形においては三平方の定理が成り立つため,3つの角が30°,60°,90°である直角三角形と,45°,45°,90°である直角三角形の3辺の長さには,それぞれ次のような関係が成り立っています。 となります。 となります。 が成り立ちます。 これを「三平方の定理」 といいます。




三平方の定理を慶應生が超わかりやすく解説 公式 証明 計算問題付き 高校生向け受験応援メディア 受験のミカタ



Mathematics 三平方の定理 2 特別な直角三角形 働きアリ
直角三角形の各辺の長さの関係はピタゴラスの定理(三平方の定理)と呼ばれる。 記号⊿を使ってあらわすことがある。 直角三角形の直角以外の2つの角を、直角三角形の鋭角 と呼ぶ。それらの大きさの和は、直角に等しい。三平方の定理直角三角形辺の長さ 四平方の定理直角三角錐面の面積 三平方の定理は, 直角三角形において,斜辺の平方は直角をはさむ2辺の平方の和に等しい と表現される. 四平方の定理を同様に表現すると,■次のような直角三角形の三辺の長さについては, a 2b 2=c 2 が成り立ちます.(これを三平方の定理といいます.) ■逆に,三辺の長さについて, a 2b 2=c 2 が成り立つとき,その三角形は直角三
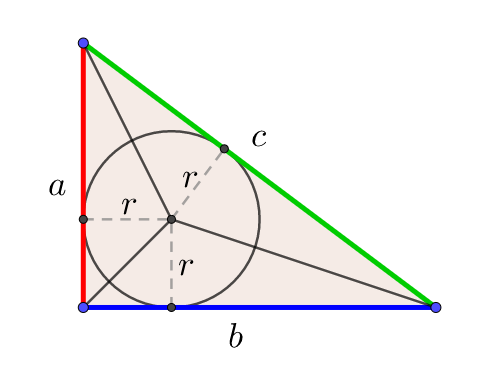



三平方の定理の証明4 直角三角形と内接円 キソカラ




三平方の定理 特別な直角三角形の3辺の比 中学数学 定期テスト対策サイト
中线定理 (pappus定理),又称 重心定理 ,是 欧氏几何 的定理,表述三角形三边和中线长度关系。 定理内容:三角形一条中线两侧所对边平方的和等于底边的平方的一半加上这条中线的平方的2倍。设三边为a,b,c 则 tanA=a/b tanB=b/a 根据数值对表查角度1、直角三角形 直角三角形是一个几何图形,是有一个角为直角的三角形,有普通的直角三角形和等腰直角 三角形两种其符合勾股定理,具有一些特殊性质和判定方法2、特殊性质・イ 直角三角形の直角をはさむ2辺の長さと斜辺 を1辺とする正方形の面積の値の関係を基に三 平方の定理を見いだし、それを証明することが できる。ワークシート記述の観察、発問に対す る生徒の発言の観察 第2時 三平方の定理を 利用する。
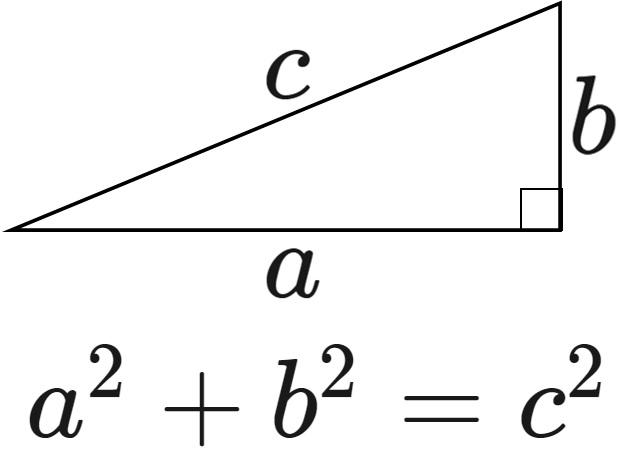



B Oc Hdjqqqofm




三平方の定理 覚えること 三角定規 苦手な数学を簡単に
勾股定理直角三角形的两直角边的平方和等于斜边的平方 等腰直角三角形三边关系 你没读过勾股定理吗?你说的等腰三角形是两直角边的平方和等于斜边的平方啊!例如a和b分别为两条直角边,c为斜边;那么它的方式是a的平方加上b的平方等于c的平方啦!这三平方の定理とは 直角三角形のときに利用できる 辺の長さの関係式でしたね。 それを発展させて考えていくと 直角三角形だけでなく 鋭角、鈍角三角形を見分ける方法として活用することができます。 入試などでは、活用する機会は少ないと思います直角三角形の選択した2つの入力値から他の要素の値を計算します。 入力指定 底辺と高さ 底辺と斜辺 底辺と角度 斜辺と高さ 斜辺と角度 高さと角度 面積と底辺 面積と高さ 面積と斜辺 面積と角度



Q Tbn And9gcq7h6dlzvq5e0plulfvxu64dpvadasyky0sizoi2drjv Uyz1m5 Usqp Cau



三平方の定理を直角三角形以外の三角形に使う時の公式ってどうなりますか Yahoo 知恵袋
一、直角三角形 勾股定理及其逆定理 (1)勾股定理:直角三角形两条直角边的平方和等于斜边的平方。 (2)勾股定理的应用:①已知直角三角形的两边求第三边; ②已知直角三角形的一边,求另两边的关系;③用于证明有关线段平方关系的问题。直角三角形是数学里最有用的形状之一! (例如,它用在 勾股定理 和 正弦、余弦和正切上。) 你来试试 (拉拽点a、b或c): 两种直角三角形 有两种直角三角形: 不等边直角三角形 一个直角 另外两个 不同的 角 没有等边 等腰直角三角形 一个直角三平方の定理に関心を持ち,直角三角形の性質を調べようとしたり,定理を活用 しようとする. 数学への関心・意欲・態度 2 直角三角形の3辺の長さの間の関係を見いだし,三平方の定理を用いて,図形の 性質を考える ことができる. 数学的な見方や考え方 3 三平方の定理とその逆




三平方の定理 ピタゴラスの定理 の計算問題 の3つの解き方 Qikeru 学びを楽しくわかりやすく




中3数学 三平方の定理 で最も重要なポイントとは 映像授業のtry It トライイット
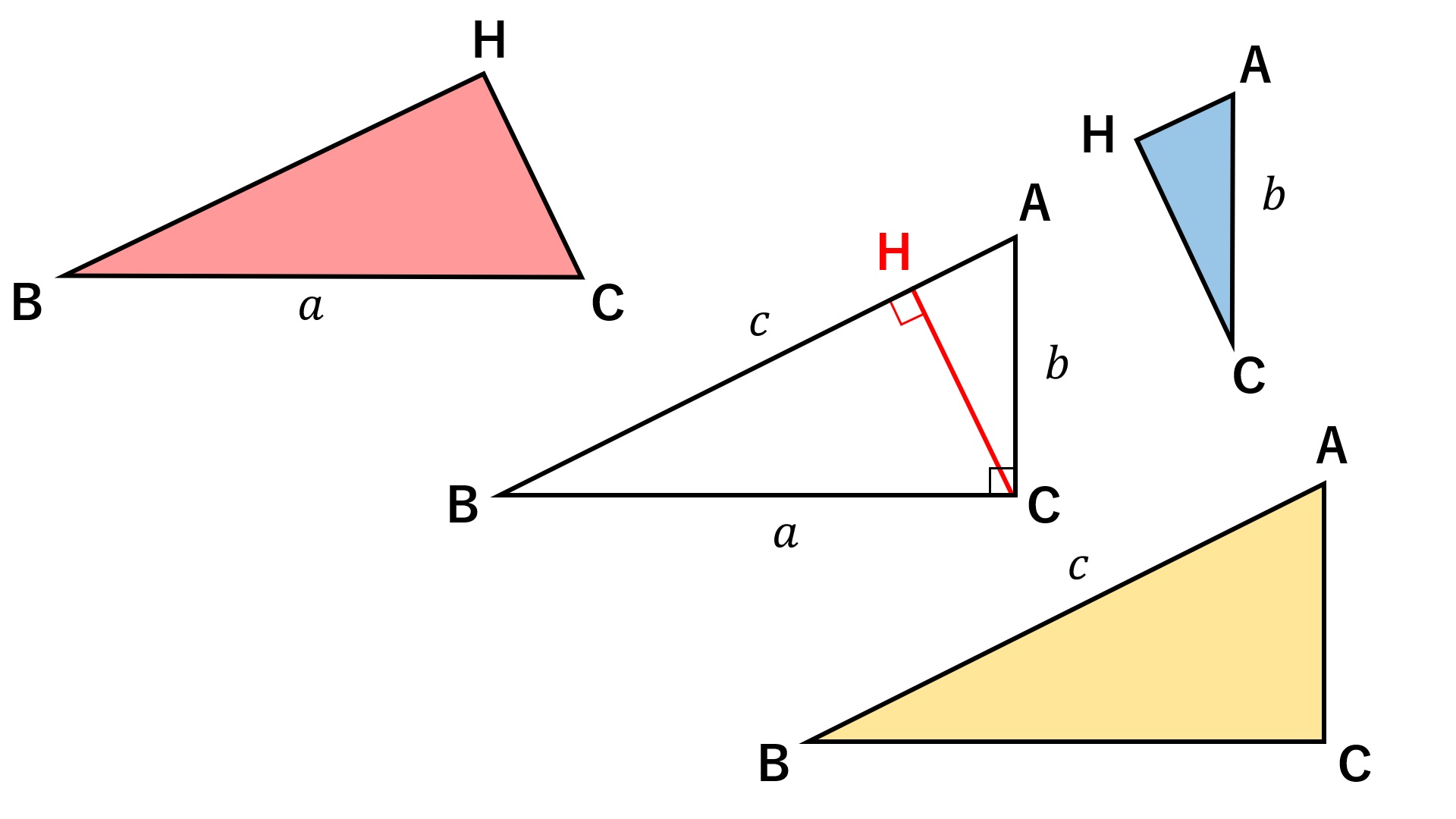
三平方の定理の証明 AB=c, BC=a, AC=b, ∠ACB=90°の直角三角形ABCと合同な直角三角形を図のように並べて正方形ABDFをつくる。 正方形ABDFの面積をSとすると、1辺がcなので S=c2 ① また、正方形ABDFは△ABCと合同な三角形4つと正方形EGHCでできている。三平方の定理_座標平面の三角形 座標上の2点A,Bの距離 A (x1, y1),B (x2, y2)とすると 線分ABの長さ = (x 1 x 2) 2 (y 1 y 2) 2 A B x y O直角二等辺三角形、三平方の定理の詳細は下記が参考になります。 直角二等辺三角形の辺の長さは?1分でわかる求め方、公式、辺の長さと角度の関係、証明 ピタゴラスの定理とは?1分でわかる意味、証明、345の関係、三平方の定理との違い 100円から読める!ネット不要!印刷しても読み




直角三角形の辺の長さ 合同条件 面積について アタリマエ




三平方の定理 おやじさん ネット
勾股定理 直角三角形两直角边(即"勾","股")边长平方和等于斜边(即"弦")边长的平方。也就是说,如果直角三角形的两直角边长分别为a,b,斜边长为c,那么 。 勾股定理只适用于直角三角形,应用于解决直角三角形中的线段求值问题。S {\displaystyle s} 等於三角形的半周長,即: s = a b c 2 {\displaystyle s= {\frac {abc} {2}}} 秦九韶 亦求過類似的公式,稱為 三斜求積法 : A = 1 4 c 2 a 2 − ( c 2 a 2 − b 2 2 ) 2 {\displaystyle A= {\sqrt { {\frac {1} {4}} {\left c^ {2}a^ {2}\left ( {\frac {c^ {2}a^ {2}b^ {2}} {2}}\right)^ {2}\right}}}} 也有用 幂和 来表示的公式:




中学3年生 数学 三平方の定理 練習問題プリント ちびむすドリル 中学生




勉強しよう数学 拡張三平方の定理




三平方の定理を使って面積を求める方法は 問題を使って解説するよ 中学数学 理科の学習まとめサイト




なぜ 三平方の定理で角度bが90度だとわかるのですか Clear
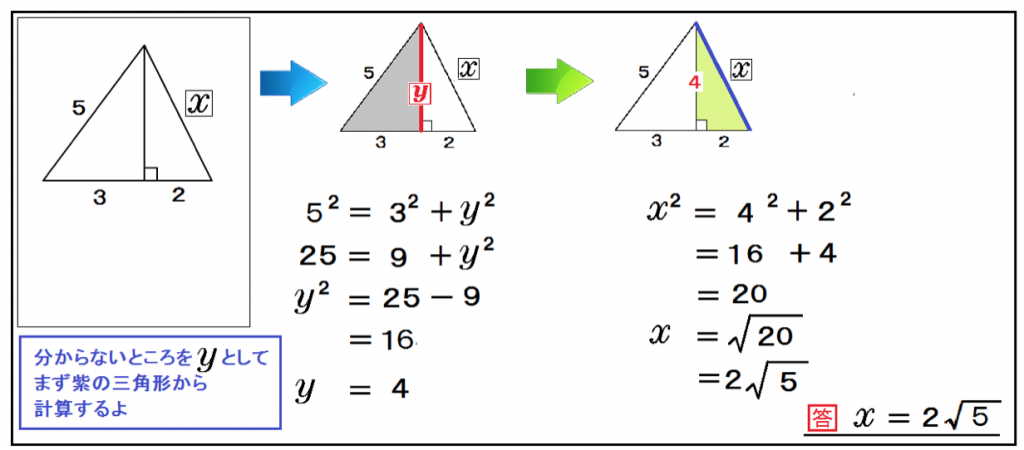



1 1 ルート2 三角形



質問にお答えします 小学生でもわかる数学とは 教育研究所arcs




エレガント直角 三角形 の 定理 最高のカラーリングのアイデア




中学数学 三平方の定理 直角二等辺三角形 オンライン無料塾 ターンナップ Youtube



三平方の定理 をシミュレーションで復習しよう 数学入門




三平方の定理 特別な直角三角形の比を使った計算のやり方は Youtube




数学 三平方の定理が成り立つ三辺の比 最重要7パターン 受験の秒殺テク 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo



中学数学 直角三角形の三平方の定理とは ピタゴラス 平方根 の定理をexcelの図形で Curlpingの幸せblog




三平方の定理の証明 相似を利用した証明1 Fukusukeの数学めも




必見 直角二等辺三角形の全てを早稲田生が図で解説 辺の長さや三角比 高校生向け受験応援メディア 受験のミカタ




三平方の定理 ピタゴラスの定理 と三角比の導入 教遊者




三平方の定理で3 4 5を習ってないのですが 簡潔に説明お願いします Clear




Excel 三平方の定理で直角三角形の辺の長さ 面積 角度を求める わえなび ワード エクセル問題集



三平方の定理 スタディーx



3分でわかる 三平方の定理の公式と証明 利用と問題例 合格サプリ



感銘を受けた数学 三平方の定理の美しき証明たち 数学 統計教室の和から株式会社




三平方の定理を慶應生が超わかりやすく解説 公式 証明 計算問題付き 高校生向け受験応援メディア 受験のミカタ




三平方の定理を簡単に理解 更に理解を深めよう 中学生 数学 公式 家庭教師のアルファ プロ講師による高品質指導



Python 三平方の定理 Unpyside



1



三平方の定理とは 証明や計算問題 角度と辺の比の一覧 受験辞典




三平方の定理について考える5 直角三角形の合同条件のひとつ 身勝手な主張




2つの直角三角形の角の和 円周率近似値の日に生まれて理系じゃないわけないだろ Knifeのblog



直角三角形とは 定義や定理 辺の長さの比 合同条件 受験辞典




三平方の定理の証明と使い方




三平方の定理 直角三角形の辺の長さを計算する4つの問題の解き方 Qikeru 学びを楽しくわかりやすく




中学3年生 数学 三平方の定理 練習問題プリント ちびむすドリル 中学生




三平方の定理で辺を求める Youtube



中学数学の最後にして最大の壁 三平方の定理はこれで満点ゲット 高校入試徹底対策ガイド




3分でわかる 三平方の定理 ピタゴラスの定理 の公式とは Qikeru 学びを楽しくわかりやすく




三平方の定理 直角三角形の辺の長さを計算する4つの問題の解き方 Qikeru 学びを楽しくわかりやすく




中3数学 三平方の定理 で最も重要なポイントとは 映像授業のtry It トライイット
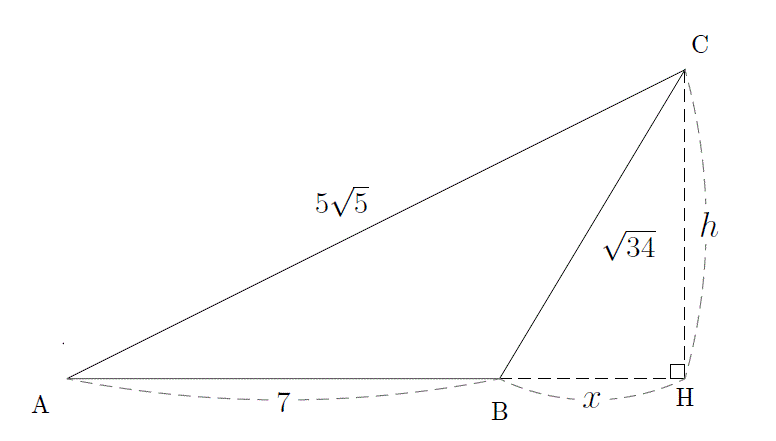



かみのドリル 三平方の定理



高校入試 英語 数学 三平方の定理の逆



1



Mathematics 三平方の定理 2 特別な直角三角形 働きアリ




直角三角形 Twitter Search




三平方の定理 特別な直角三角形 イ弋マ本ゼミナール




三平方の定理 無料で使える中学学習プリント




三平方の定理を直角三角形二つで証明 Youtube



直角三角形ではない場合ピタゴラスの定理はどう使えるのでしょうか Quora



Ppt 6 三平方の定理 Powerpoint Presentation Free Download Id




三平方の定理の計算 この問題は絶対にできるようになろう 中学や高校の数学の計算問題




数学 中3 61 三平方の定理 基本編 Youtube



三平方の定理の導入 Geogebra




感銘を受けた数学 三平方の定理の美しき証明たち 数学 統計教室の和から株式会社




中3数学 三平方の定理 で最も重要なポイントとは 映像授業のtry It トライイット




三平方の定理の証明と使い方



中学数学 直角三角形3 4 5以外に知ってる




三平方の定理 ピタゴラスの定理 と公式の証明 忍者が用いた三角の知恵 アタリマエ




中学数学 三平方の定理 特別な直角三角形 中学数学の無料オンライン学習サイトchu Su



感銘を受けた数学 三平方の定理の美しき証明たち 数学 統計教室の和から株式会社




3分でわかる 三平方の定理の公式と証明 利用と問題例 合格サプリ




三平方の定理を慶應生が超わかりやすく解説 公式 証明 計算問題付き 高校生向け受験応援メディア 受験のミカタ




三平方の定理 覚えておきたい基本公式を解説 数スタ




三平方の定理を英語で読んでみる




三平方の定理 自動計算サイト




三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学




押川 隼也 高校 大学受験対策 Su Twitter 証明シリーズ 三平方の定理 直角三角形の斜辺の長さをc 残りの二辺の長さをそれぞれaとbとおくと C 2 A 2 B 2 なんで と思った人も多いかと思ったので 実際に証明してみました 理解できた人rt T Co




三平方の定理 ピタゴラスの定理 とは 応用問題パターンまとめ10選 遊ぶ数学
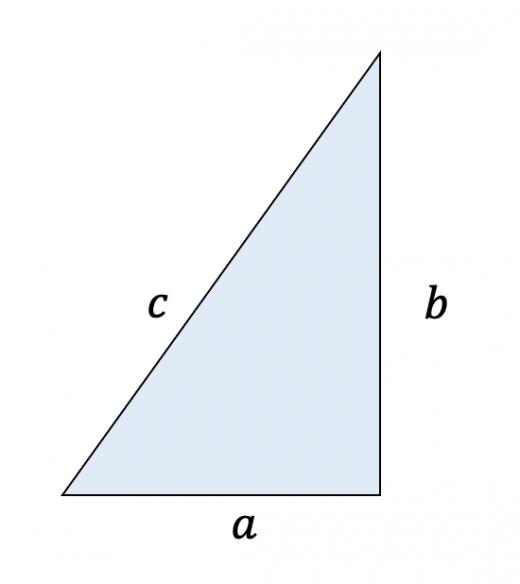



直角三角形の定義とさまざまな公式 高校数学の美しい物語



三平方の定理が一瞬で理解できる 公式 証明から計算問題まで解説 Studyplus スタディプラス



三平方の定理の最も変わった証明方法はなんですか Quora




三平方の定理 ピタゴラスの定理 と三角比の導入 教遊者



中学数学の最後にして最大の壁 三平方の定理はこれで満点ゲット 高校入試徹底対策ガイド




交流回路でよく使う三角形の比 電験三種講座の翔泳社アカデミー




三平方の定理 ピタゴラスの定理




三平方の定理 ピタゴラスの定理 と三角比の導入 教遊者



円を利用した三平方の定理の証明 数学の面白いこと 役に立つことをまとめたサイト




三平方の定理の証明と使い方




三平方の定理 ピタゴラスの定理 の計算問題 の3つの解き方 Qikeru 学びを楽しくわかりやすく




特別な直角三角形の辺の比 無料で使える中学学習プリント




三平方の定理 ピタゴラスの定理 の公式と計算方法 リョースケ大学



三角形の内角30度 60度 90度のとき辺の比は1 2 Root3になる Yahoo 知恵袋




必見 直角二等辺三角形の全てを早稲田生が図で解説 辺の長さや三角比 高校生向け受験応援メディア 受験のミカタ




数学 三平方の定理が成り立つ三辺の比 最重要7パターン 受験の秒殺テク 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




中3数学 三平方の定理 で最も重要なポイントとは 映像授業のtry It トライイット




数学 三平方の定理が成り立つ三辺の比 最重要7パターン 受験の秒殺テク 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo
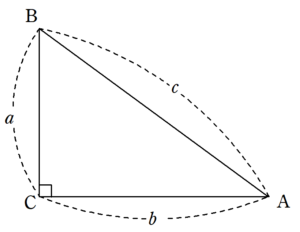



三平方の定理の証明 ユークリッドの証明 Fukusukeの数学めも




数学 三平方の定理が成り立つ三辺の比 最重要7パターン 受験の秒殺テク 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




三平方の定理およびその逆 証明 理数系無料オンライン学習 Kori



三平方の定理 やややさしい数学




三平方の定理の証明と使い方




カーナビはなぜ正確なの その秘密 三平方の定理 で教えます 横山 明日希 ブルーバックス 講談社 1 4




三平方の定理 特別な直角三角形の3辺の比 中学生からの勉強質問 数学 進研ゼミ中学講座




Excel 三平方の定理で直角三角形の辺の長さ 面積 角度を求める わえなび ワード エクセル問題集



0 件のコメント:
コメントを投稿