例題 上節でみたように,$2$ 円の位置関係を調べるには,$2$ つの円の半径と,中心間の距離を調べればよいのでした.円の方程式からその中心の座標と半径を求める方法は前記事 →円の方程式の表し方 で紹介しています.これらの知識を用いて,実際にいくつかの例題を解いてみましょう. 円を中心から描くには 図形を作成すると、ドラッグしたときに図形の角になる部分から描画されます。 図形の中心から描画するには、Ctrlキーを押しながらドラッグします。 Ctrlキーを使うと、円だけでなく、ほかの図形も中心から描画できます円中心算出部32で、データ組の3点を通る円の中心点を各データ組について求める。 例文帳に追加 The circle center calculating part 32 calculates the central point of a circle passing through three points in each set of data 特許庁

数学 円弧から円の中心が割り出せるのかを検証してみた 円弧のトレース用
円の中心座標
円の中心座標-三角形の外心、三角形の外接円 この1点で交わった点 o を三角形の外心という。 外心 o を中心として、半径 oa の円が三角形 abc の外接円である。 oa=ob=oc ol⊥bc 、 om⊥ac 、 on⊥ab数学 において、 円 (えん、 英 circle )とは、 平面 (2次元 ユークリッド空間 )上の、定点 O からの距離が等しい 点 の集合でできる 曲線 のことをいう。 ここで現れる定点 O を円の 中心 と呼ぶ。 円には、その中心が1つあり、また1つに限る。




中学数学 3点を通る円の中心の書き方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
中心線の引き方 その2 円の中心線の引き方 その3 外部変形を使う 今回は、別の方法を紹介します。 中心線コマンドとクロックメニューの円周1/4点を使います。 円の中心線の描き方 中心線 ―円上で、右クリック0時の方向にドラッグ外接円、外心について 「外接円」や「外心」の用語や意味は中学の 教科書の発展内容としてあります。 それぞれの各辺の垂直二等分線は一点でまじわり、その点Dを中心に円を書くと Dを中心に三角形の3つの頂点を通る円を書くことができて、この円点 (−a ,−b) を中心とする半径 r の円の方程式が (xa)2 (yb)2=r2 点 (a ,−b) を中心とする半径 r の円の方程式が (x−a)2 (yb)2=r2 のように,中心の座標 (a , b) は,円の方程式では見かけ上の符号が逆になる点に注意. (1) (2)とも右辺は r2 なので, 半径が 2
円(中心半径) 円を作図します。 コマンド選択後、ダイアログが表示され 半径2点直径2点円周3点のそれぞれから、作図方法を選択できます。 半径2点 最初の1点目は円の中心点になります。 次の点で円周上点、または半径を指示でき中心(ちゅうしん)とは、一般に図形のちょうど真ん中に位置する1点のことをいい、円や楕円、球などの図形では重心に一致する。 記号では原点(origin)を表す O や、center の頭文字の C と表記されることが多い。 概要 円の場合は中心から円周上の点までの距離は一定であり、それは円のJw_cadで描いた円と円の中心線を描いたり単独円の中心線を描くときの使い方を練習しましょう。 (^o^ )/ Jw_cadで描いた図面の中に二つの円を描いたとして、その中心に線を描いたり、ひとつの円の中心線を描いたりすることもあると思いますけど、その時どう使えばいいのか練習したいと思います
3点を通る円POINT 円の通る3点から中心・半径を求める一般式を導出する. 導出した式で計算フォームを作成. Excelにコピペして使えるフォーマットあり. 単純な「連立方程式」の問題ですが,一般解は少し複雑な形になります. 計算フォーム Excel用フォーマット 導出 円の方程式 円の中心 円中心:原点,半径:r の円の方程式 x 2 y 2 = r 2 r と θ を使って円周上の点Pを表すと, {x 円の中心を求める まずは、中心を求めたい円の周上にコンパスの針の部分を置いて、 少し大きめの半円を書くよ 周上の他の場所にも、コンパスの針を置いて さっきと同じ大きさの半円を書くよ そして、半円2つが重なった2点を結ぶ線を引くよ 最後に




最後の2円の中心間の距離の求め方が分かりません Clear




扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ
円の半径とは、円の中心から円周上の任意の点を結んだ線の長さです。 半径を最も簡単に求める方法は直径を2で割ることです。 直径がわからなくても、円周 ( C = 2 π r {\displaystyle C=2\pi r} )や円の面積 ( A = π r 2 {\displaystyle A=\pi r^ {2}} )など他の値が与えられそこで今回は、すでに描いた円の中心点を簡単にだす方法をご紹介させていただきます。 円の中心点を簡単に出す方法 今回使用するJw_cadの便利な機能は『 クロックメニュー 』という機能です。 まずは、キャプチャー動画で操作手順をご確認ください。円の中心は、次の方法で求めることができます。 メニューから、 作図 点と進み、 コントロールパネルの 仮点にチェックを入れます。



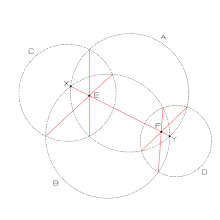
アポロニウスの円の中心と半径



アポロニウスの円の中心と半径
円の方程式 中心:原点,半径:r の円の方程式 ; 中心点のサーチマークを確認して円をクリックします。 円の中心点を通過する補助線が作図できました。 メカニカルキットfor図脳RAPID Ver3 以降をお持ちの場合は、「関連する記事」もご参照ください。例として,中心が (0, 0) (0,0) (0, 0) で半径が 2 2 2 の円の方程式を考えます。
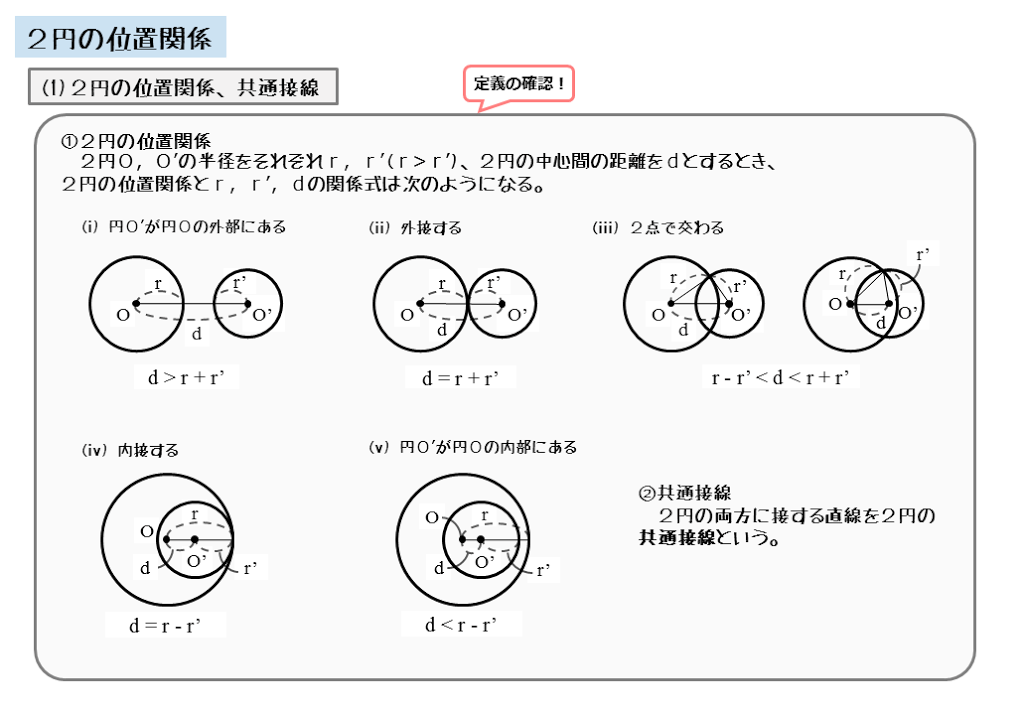



図形の性質 2円の位置関係について 日々是鍛錬 ひびこれたんれん



3
一つの弧に対する「円周角」の大きさは,「中心角」の半分になります. OC=OB= (半径)だから OBCは二等辺三角形になる. 二等辺三角形の2つの底角は等しいから ∠ B=∠ C (1) ∠ BOA=∠ B∠ C (2) 差で示します. 中心角92°が書いてあって,円周角が垂直2等分線 次のような問題があったとしましょう。 上の図において、円の中心oを図示しなさい。 このような問題の場合には、垂直2等分線を用いて中心oの位置を求めることができます。 垂直2等分線のおさらい 垂直2等分線とは、下図のよ空き缶の中心の見つけ方 1、空き缶の円を紙に写し取ります。 直角の物(ハガキなど)を置きます。 (Pの位置) 3、直角の物と円が交わる2点に印を付けます。 (AとB) 4、AとBを結んだ線の真ん中の点が、この円の中心になります。 (Oの点) 5、紙を
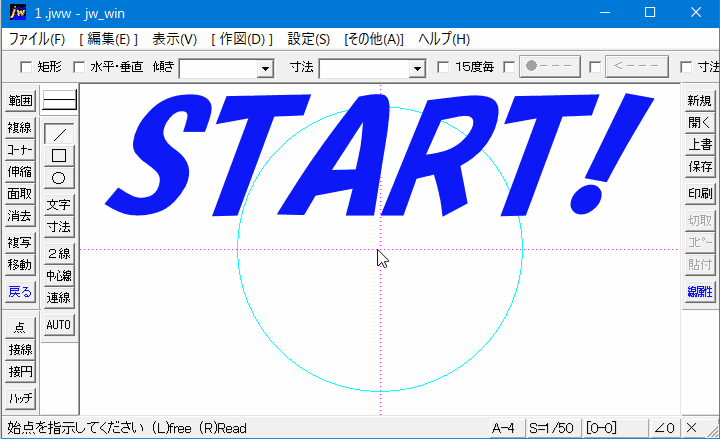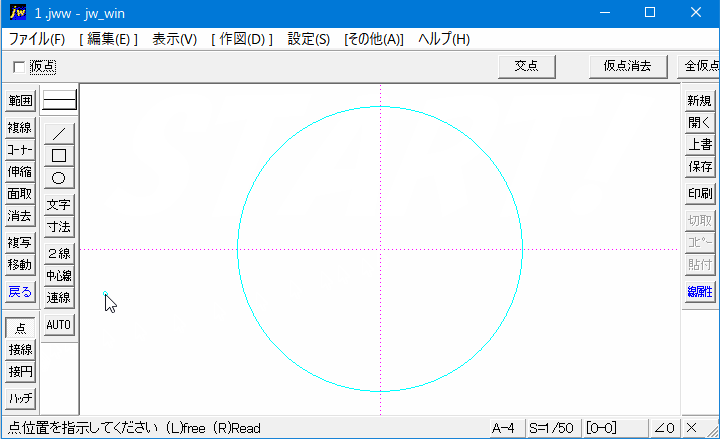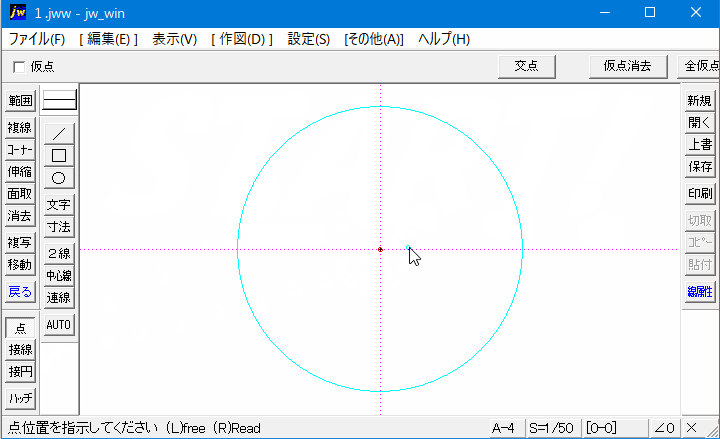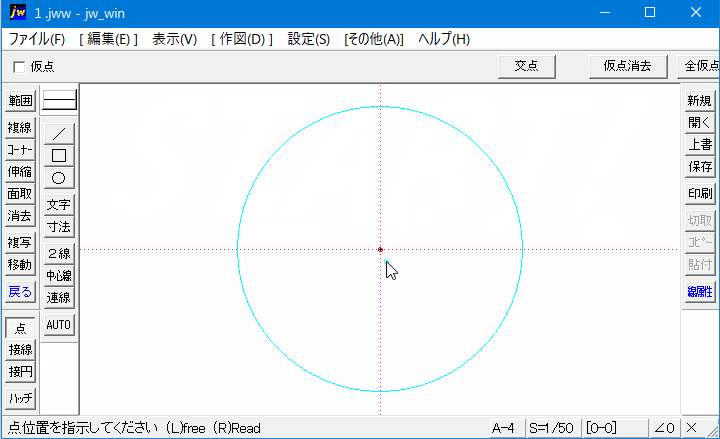



Jw Cad 円の中心点の出し方




第3巻命題1 円の中心の作図 Stoixeia ストイケイア
中心(a,b)で半径r、円周の任意の点を(x i,y i)とすると円は以下の式で表せます。 rと中心とx i,y i 間の距離の差を出す式をとりあえず差を0として作成します。 上記の式を二乗すると 左式を使って上式からカッコを取り除きシンプルにします。中心マークは、円または円弧の中心マークし、図面でジオメトリ サイズを説明するアノテート アイテムです。 中心マーク ツールを使用すると、円形エッジに中心マークや中心点を追加できます。 中マークの線は、寸法を配置する際に参照できます。 例円の中心は正しく配置されており、対応する半径も実際のチップとうまく一致しているようです。しかし、まだ検出されていないチップがかなりあります。Sensitivity' をもう少し高い 092 に上げてみま




中学数学 3点を通る円の中心の書き方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




イラスト豆知識 円の性質 株式会社オプライン
すなわち,上記の偏心(a,b)を決定し,それを中心と した同心円でワーク形状を挟んだ場合の半径差が真円度と なることを意味している. 5.真円度と基準円 真円度の求め方には,基準円を元に以下の4つの方法が ある3). 1.最小領域真円度/最小領域基準円円を2つに折ると折り目の線が中心をとおることを基にして、円の中心の見つけ方を説明する考 (2)本時の展開(3/8) 過程 主な学習活動と予想される児童の反応 ――研修との関わり ⋯⋯⋯⋯評価 つかむ 考える 深める円を書くことができます。 この円を 内接円といい、中心を内心といいます。 下の「定理8」は三角形の3つの角の二等分線は1点で交わること の証明ですが、その証明方法をはじめてみる方にとっては、「へぇ~ 垂線か」と思われるかもしれませんが




円の中心の出し方 コンパスなし 直径わからない編 シャンハイ山本弾工房




2つの円の位置関係と円の半径 中心間の距離 高校数学の知識庫
図形ツールの直接描画で描画したものを中心で合わせる 機能はございません。 拡大、縮小を行う際は、Altキーを押下で中心を基準に 拡大縮小が可能です。 また、同心円定規で閉じた円が描けないとのことですが 下記の画像は同心円定規を2つ重ねた中心マークは、円の中心をマークし、図面でジオメトリ サイズを説明するアノテート アイテムです。 '中心マークと中心線' を SOLIDWORKS ナレッジベースで検索します。 ヘルプに関してフィードバックを送信することができます。 しかし 円同士の関係は中心間の距離と半径で決まる 見出しにもあるとおり、円同士の関係を決めているのは 2つの円の中心の距離 と 2つの円の半径 です。例えば円同士が全く交点を持たない場合というのは一つ目に こんなのが考えられます。




円の接線 円の中心が原点でないとき の解き方をマスターしよう 高校数学 図形と方程式 数学の部屋 Youtube
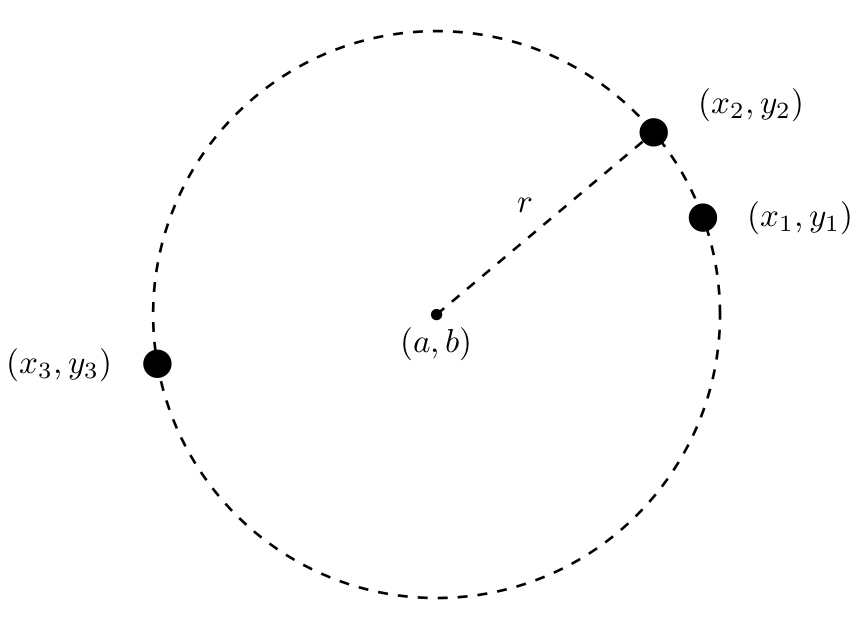



3点を通る円の中心と半径 Notes Jp
2点と半径から円の中心を求める 2点の座標と半径を入力すると、指定した半径で2点を通る円の中心座標が表示されます。 2点間の距離 < 半径×2 → 中心が2つ 2点間の距離 = 半径×2 → 中心が1つ(1点目と2点目に同じ座標が表示される)理論¶ 円を表す式は となります.ここで は円の中心, は円の半径を表します.円を表すにはこの三つのパラメータを使うので3次元積算機が必要になりますが,これは非効率的です.OpenCVは巧妙な方法 Hough Gradient Method を使ってエッジの勾配を使います. 円検出に使う関数は cv2HoughCircles4 以下の図で,点oは円の中心,点pは円周上の点である。このとき,点pにおけるこの円の接線をコン パスと定規を使って作図しなさい。ただし,作図するためにかいた線は消さないでおきなさい。 ンパスと定規を使って作図しなさい。



幾何計算 2点と半径から円の中心点を求めます Satoh
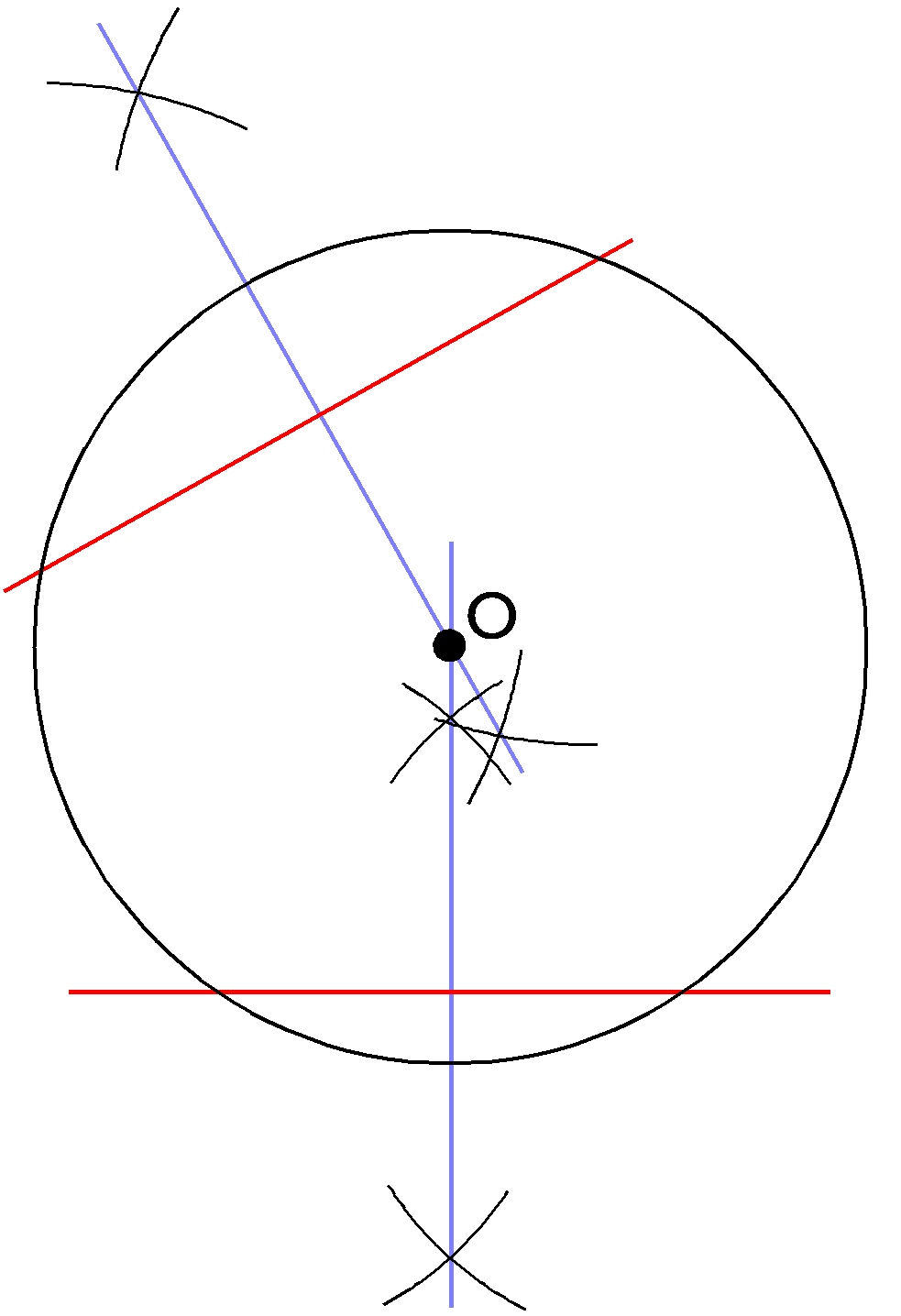



円の中心 Wordで数学問題プリントを作ろう




中学数学 円の中心の出し方 コンパス編 サクッとわかる なぜか分かる はかせちゃんの怪しい研究室
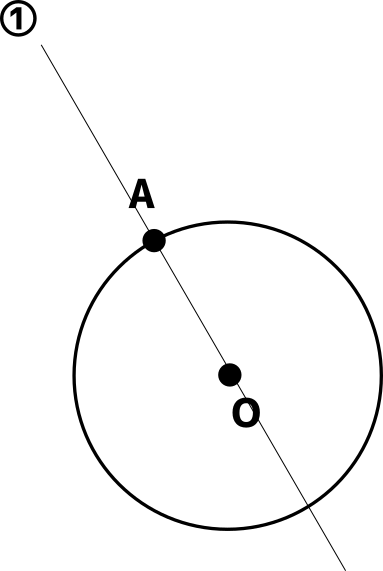



円の作図と円の接線の作図 チーム エン




1秒で出来る Jwcadで円の中心を取る方法 ほか線や四角 任意の点の中心の取り方もご紹介 注文住宅設計士の日常




円の名称 弧 弦 数学ノート




三角定規で円の中心を作図 おときち副塾長 電脳空間学習塾かもん Youtube




差し金テク 円の中心と直径を限りなく正確に求める方法 男のレシピ帳



Studydoctor円の公式と なぜ 中学1年数学 Studydoctor




円の弧と弦にまつわる性質 数学a By Okボーイ マナペディア
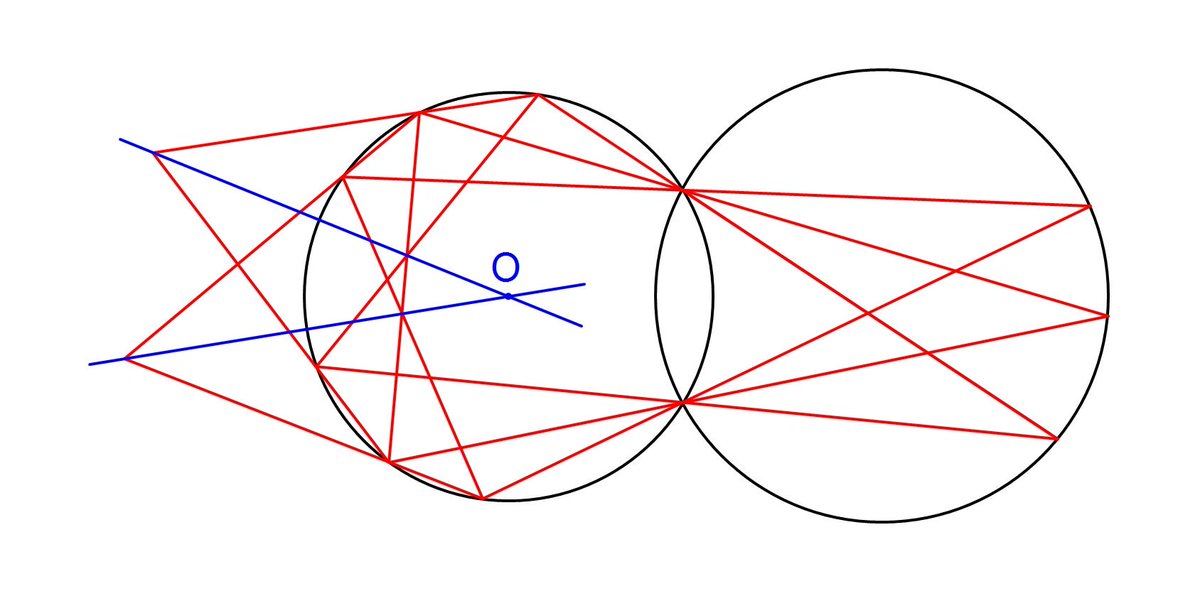



ポテト一郎 円の中心を定規のみで作図することは出来ない しかし もう1つ円があったならどうなるだろう 2点で交わる 円の中心を作図しなさい 最近知ったのだが この作図は定規のみで可能である とても美しい作図だと思うが 同意してもらえるだろ
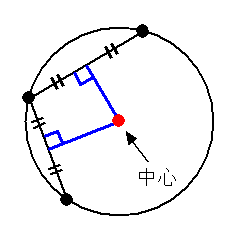



3次元空間での円の中心の求め方 Inak Engineering Llc



欠けたお皿の中心




中学数学 3点を通る円の中心の書き方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




垂直二等分線を使って円の中心をもとめる 中学数学 By Okボーイ マナペディア




3点を通る円を求める Qiita



円の一部の孤から その円の中心を求めるにはどうしたらよいでし Yahoo 知恵袋
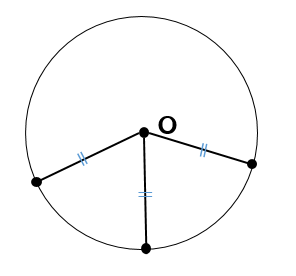



中1 作図 円の中心を求める方法を解説 数スタ
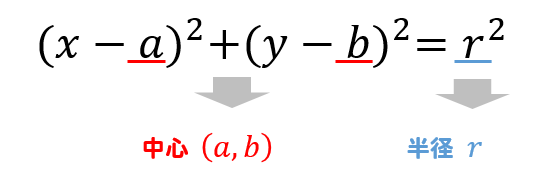



円の方程式 中心の座標と半径の求め方を解説 数スタ




標準 円の接線と作図 なかけんの数学ノート




中3数学 円の中心と弦との距離 練習編 映像授業のtry It トライイット




数学 円弧から円の中心が割り出せるのかを検証してみた 円弧のトレース用



円の中心の求め方 Love金沢水彩画
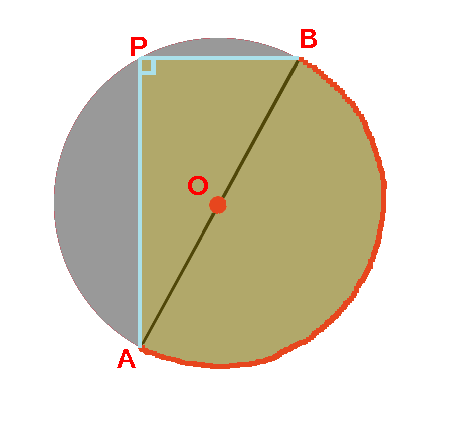



空き缶の中心の見つけ方 綿菓子を自宅で作ろう



From灘 円の中心の求め方 朝日小学生新聞 中学受験eye 関西圏




円周角の定理と証明 中心角の求め方を詳しく解説 Rikeinvest
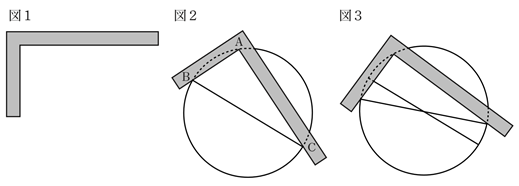



曲尺を使い円の中心を求める 1 準2級 カワズの数学ノート 数学検定 準2級
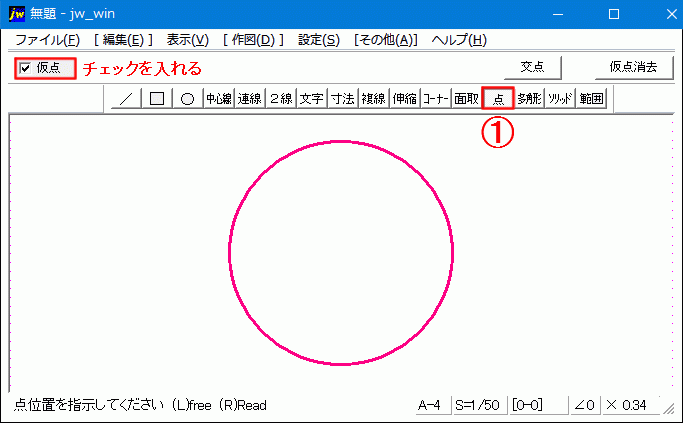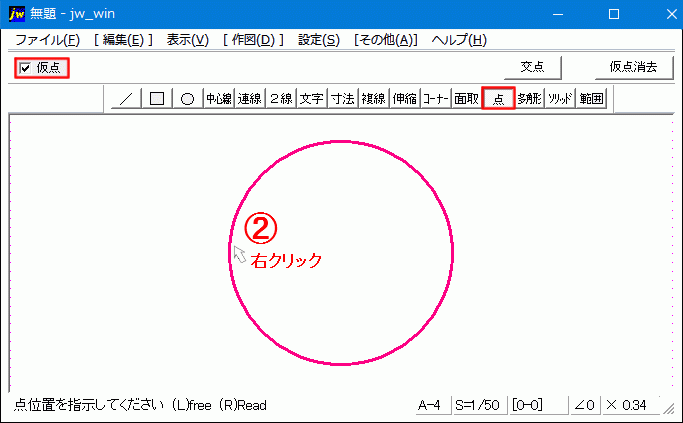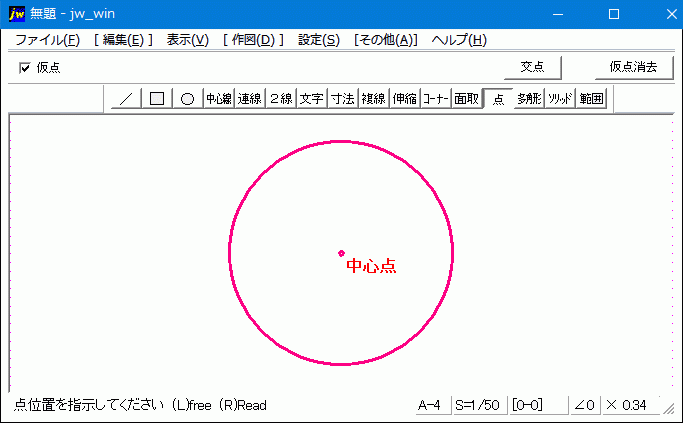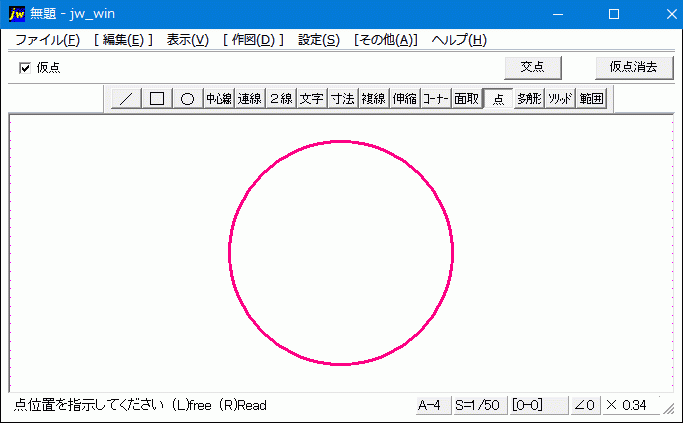



Jw Cadで円や矩形の中心点を出す方法




数学 円弧から円の中心が割り出せるのかを検証してみた 円弧のトレース用



円の方程式とは 公式 接線 微分 や半径の求め方 計算問題 受験辞典




この問題の作図の仕方教えてください 答え見てもよく分からないんですよねhahawちな Clear



1




基本 円の方程式 なかけんの数学ノート




3年算数 円と球 円の中心を見つけよう Youtube




円の中心の座標と半径を求める問題です 答えと解説を画像付きで送ってください Clear




二円の交点を結ぶ直線からの距離の比 香料ゐっすゐの夢




中3数学 円の中心と弦との距離 例題編 映像授業のtry It トライイット




楕円と円の中心 Circles Ovals 塾長の日記
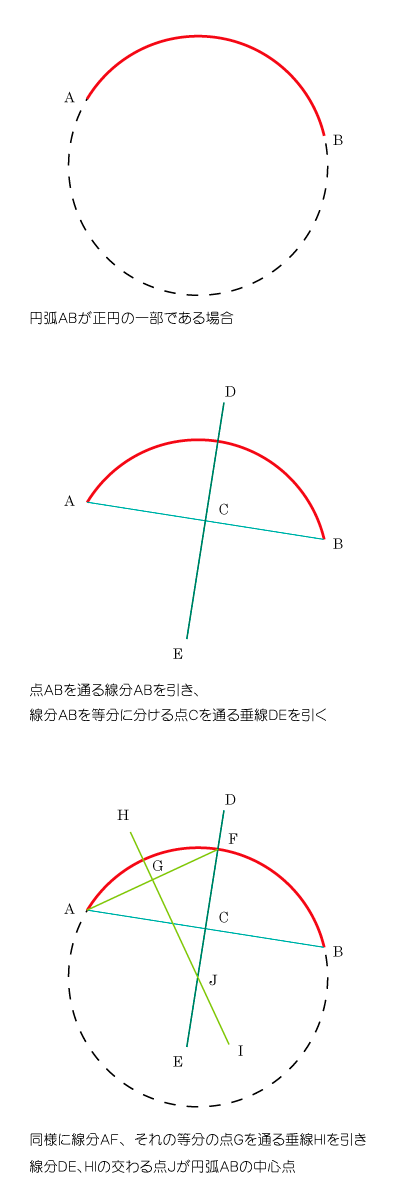



数学 円弧から円の中心が割り出せるのかを検証してみた 円弧のトレース用




中3数学 円周角の定理 の3大重要ポイント 映像授業のtry It トライイット



Www City Hadano Kanagawa Jp Www Contents Simple C004 Pdf




垂直二等分線を使って円の中心をもとめる 中学数学 By Okボーイ マナペディア




数 図形と方程式 円の中心 直線の距離 と 半径 の関係 オンライン無料塾 ターンナップ Youtube




Euclidea 1 6 円の中心の作図 解説 みのまわりのものたち
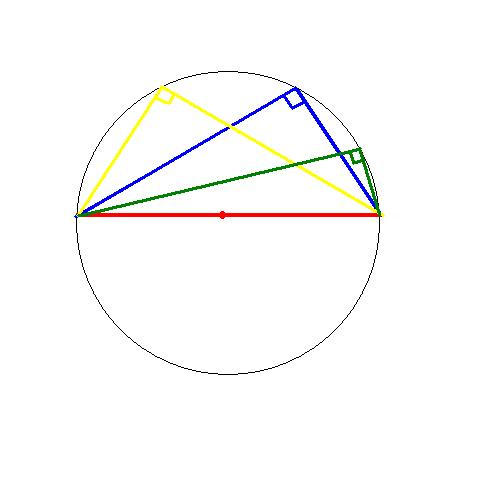



空き缶の中心の見つけ方 綿菓子を自宅で作ろう



1



円 数学 Wikipedia
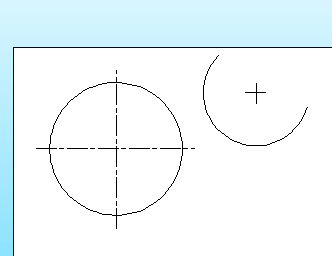



円 円弧の中心マーク 中心記号 の記入 Rootpro Cad



アポロニウスの円の中心と半径
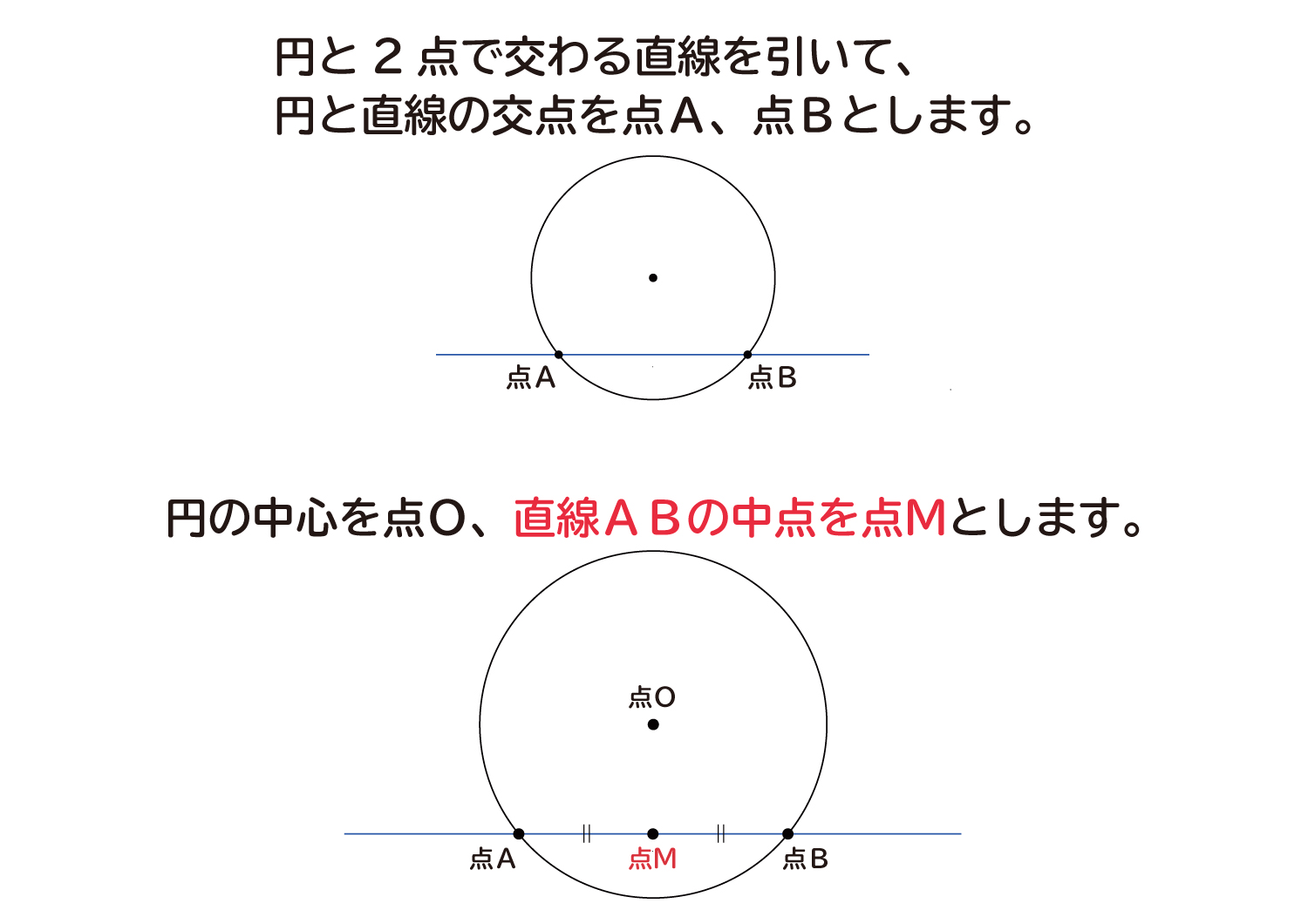



なぜ 円の接線は 接点を通る半径に垂直 になるのか を説明します おかわりドリル




3年算数円と球 1 わかる教え方コンパスの使い方




1秒で出来る Jwcadで円の中心を取る方法 ほか線や四角 任意の点の中心の取り方もご紹介 注文住宅設計士の日常



円の中心を作図



最初から丸く加工されている木材を買いました 製作したいものが円の中心を正確 Yahoo 知恵袋




中3数学 円の中心と弦との距離 練習編 映像授業のtry It トライイット




2直線の関係 三角形の外接円の中心の座標 Schoolmath S Diary




基本 2つの円の共有点 中心間の距離に注目 なかけんの数学ノート




標準 3点を通る円の作図 なかけんの数学ノート
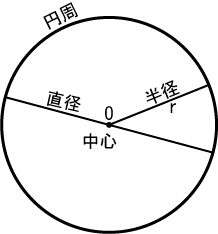



円 数学 Wikipedia



2点を通り半径rの円の中心を求める




5分で出来るセンター出し定規



1




中学数学 3点を通る円の中心の書き方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




円の方程式の求め方まとめ パターン別に解説するよ 数スタ
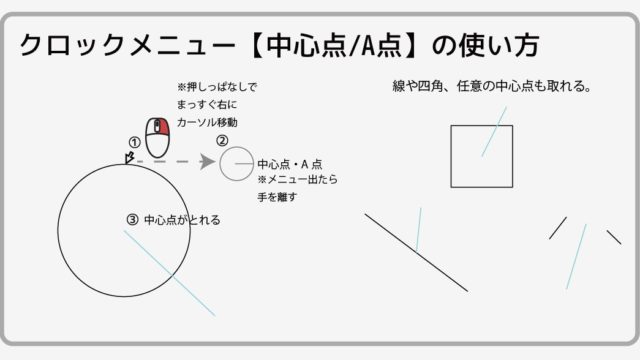



1秒で出来る Jwcadで円の中心を取る方法 ほか線や四角 任意の点の中心の取り方もご紹介 注文住宅設計士の日常
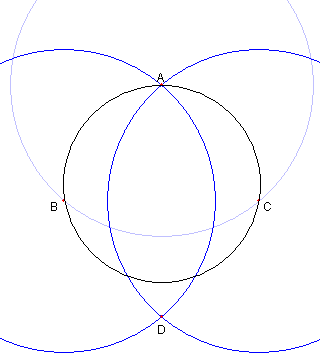



コンパスのみを使う作図




円の中心を求める 3つの方法 Wikihow



円周上の3点から円の中心を求める




数学 円弧から円の中心が割り出せるのかを検証してみた 円弧のトレース用



曲尺 かねじゃく の使い方 監督が教える工具の使い方




円の中心の作図 コンパスを使って求める方法とは 中学数学 理科の学習まとめサイト
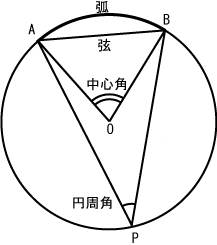



円 数学 Wikipedia



3点から円の中心と半径を求める Satoh
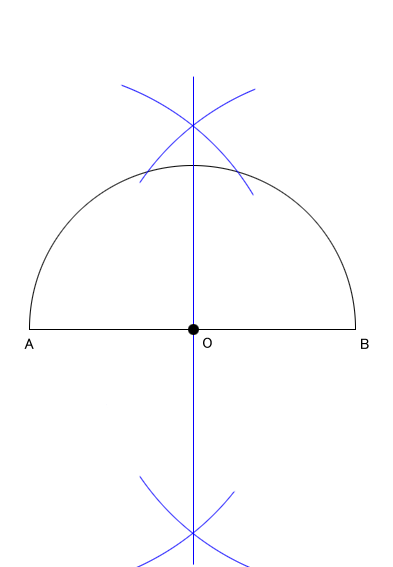



平面図形 おうぎ形 4 ネット塾
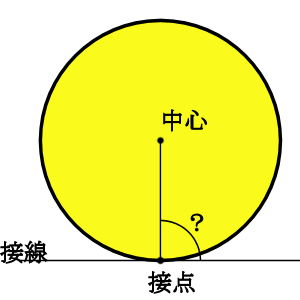



円と接線



半径1 中心角60 のおうぎ形に内接する円の半径を求める 数楽者のボヤキ ツブヤキ ササヤキ 中学 数学 道徳 Mathematics Puzzles
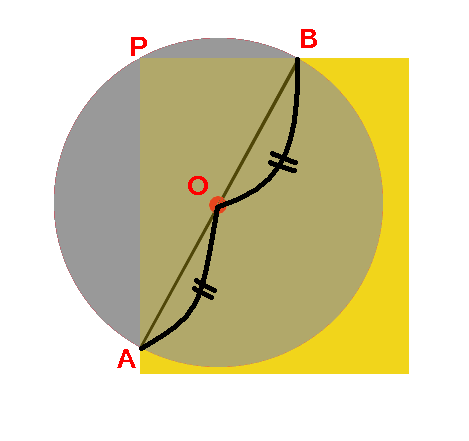



空き缶の中心の見つけ方 綿菓子を自宅で作ろう
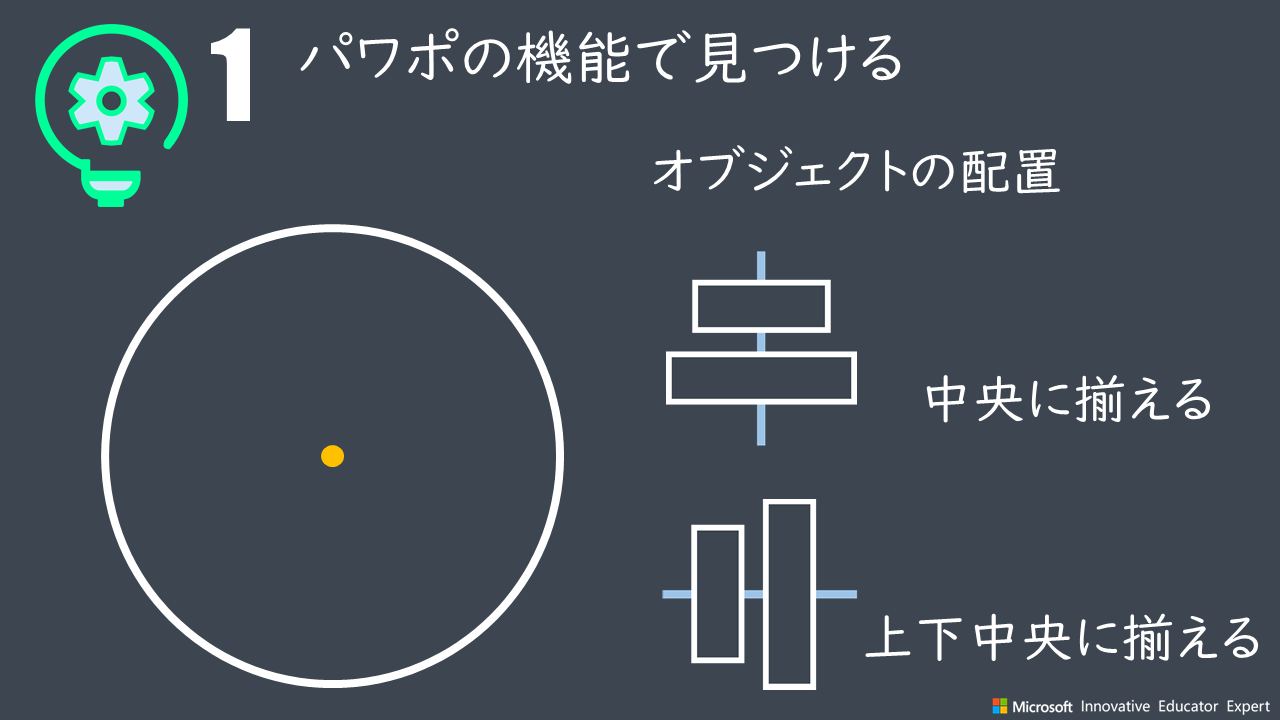



パワーポイントで円の中心を見つける つくる ict 10年までpcできなかったマイクロソフトmvpのブログ



幾何計算 2点と半径から円の中心点を求めます Satoh




円の中心の軌跡とは なんですか Clear




3点を通る円 の作図方法 コンパス 定規 数学fun
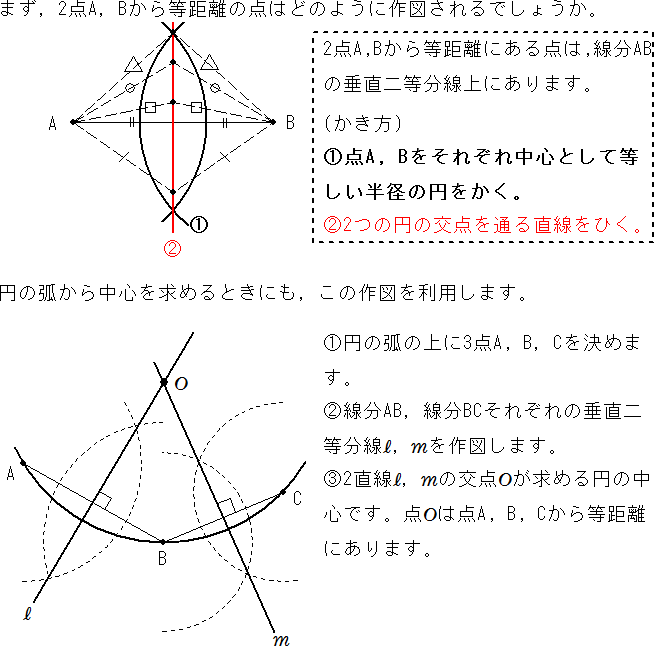



平面図形 円の中心を求める作図 中学数学 定期テスト対策サイト



Jww再入門
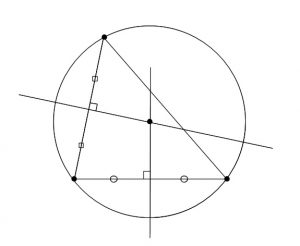



3点を通る円 と 2点とある直線上に中心がある円 の方程式の求め方




基本 円と直線の共有点 中心からの距離に注目 なかけんの数学ノート




円の中心角 弧 弦 Jsciencer




高校数学 円と直線の位置関係の分類 映像授業のtry It トライイット




外接円の方程式の求め方 数学の偏差値を上げて合格を目指す
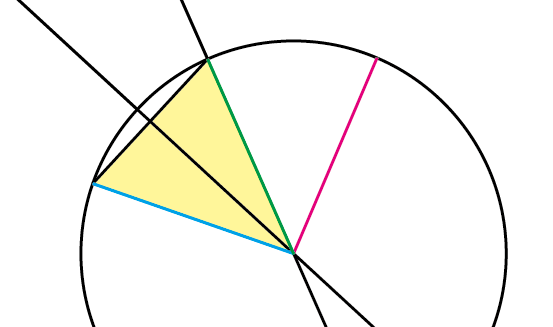



数学 円弧から円の中心が割り出せるのかを検証してみた 円弧のトレース用




中学数学 3点を通る円の中心の書き方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



0 件のコメント:
コメントを投稿