
数学 三平方の定理が成り立つ三辺の比 最重要7パターン 受験の秒殺テク 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo
二等辺三角形の定理(性質) 2つの辺が等しいと、いくつかの定理(性質とも言います)ができます。 二等辺三角形の底角は等しい 二等辺三角形の頂角の二等分線は底辺を垂直に二正弦定理から,三角形の辺の長さを求める計算について ABCにおいてa = 3 ,A = 60°,B = 45°のときbを求めよ。 という問題がありますが, これを定理にあてはめていって, b = 3 / sin60°× sin45°
三角形 辺の長さ 定理
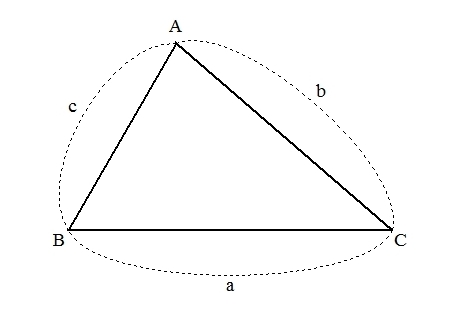
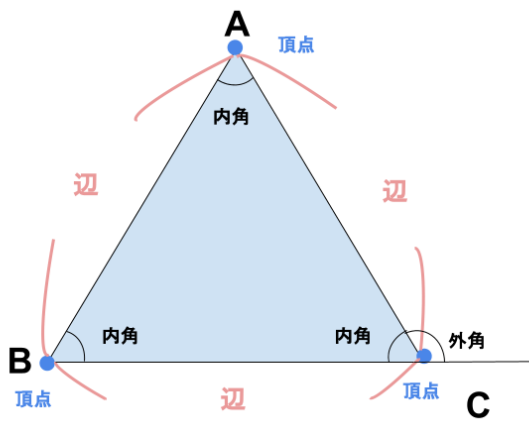
三角形 辺の長さ 定理-三角形の面積のお話 ・・・sin,cos,tan が出てこない話・・・ 三角形の面積と、内接円の半径、傍接円の半径と三角形の周の長さの半分s との関係 23 ピックの定理のお話 小学生でも分かる多角形の 三角形とは3つの線からなる図形です。 3点を頂点、3つの線分を辺といいます。 2つの辺のなす角を内角、外側にできる角を外角といいます。 三角形には以下の特徴があります。

高校数学 直角三角形を用いた三角比 Sin8 Cos8 Tan8 の定義とその理由 30 45 60 の三角比 受験の月
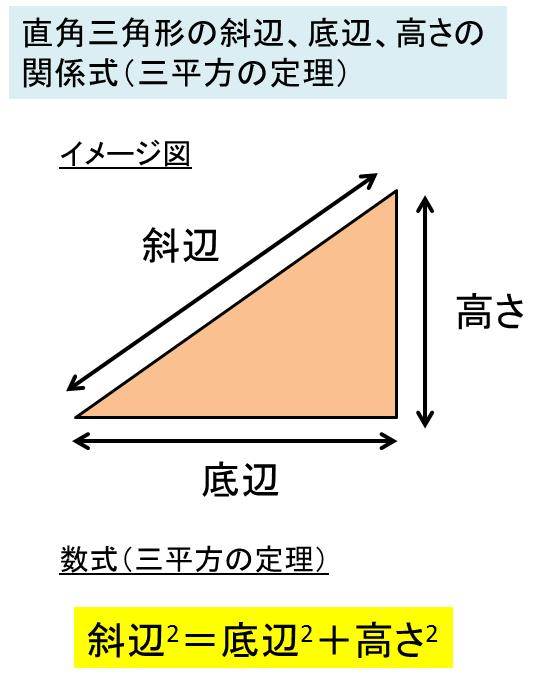
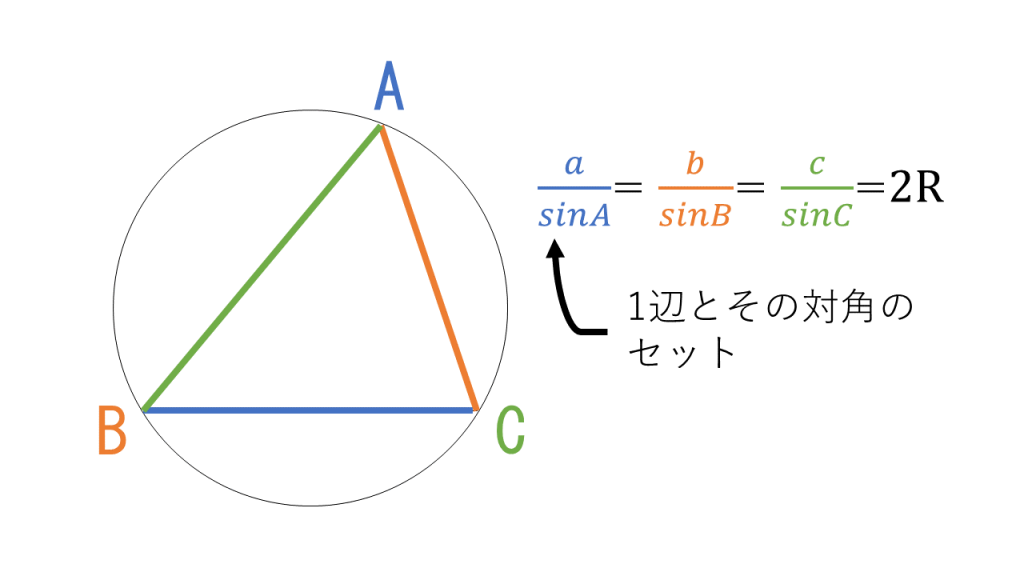
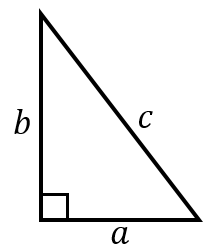
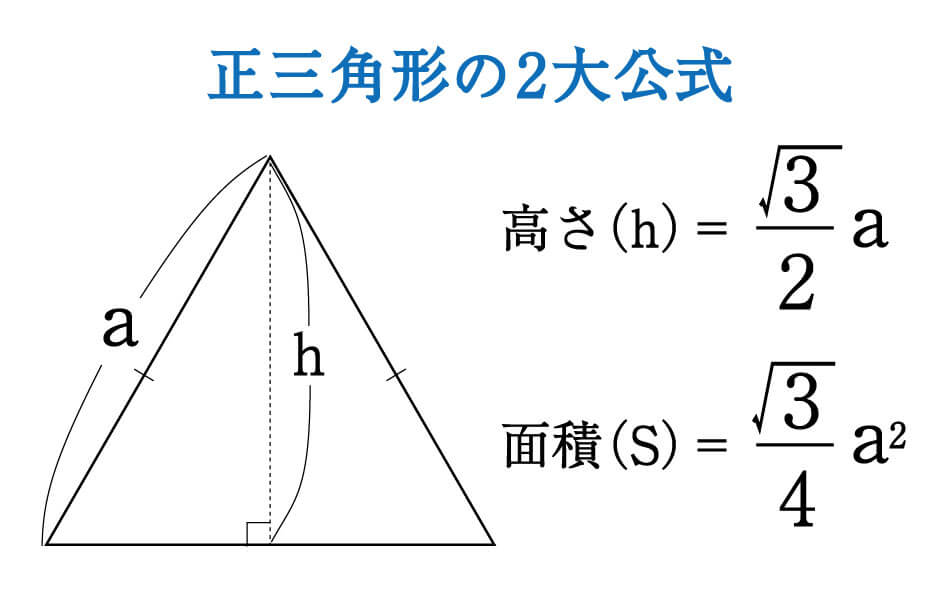
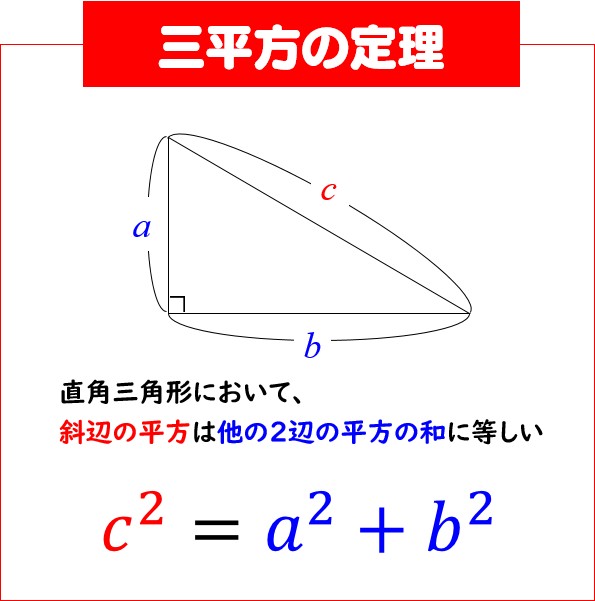
もくじ 1 三角形は必ず外接円をもつ 11 正弦定理により、sinθで辺の長さや角度、外接円の半径がわかる;初等幾何学における ピタゴラスの定理 ( ピタゴラスのていり 、 ( 英 Pythagorean theorem )は、直角三角形の3辺の長さの関係を表す。 斜辺の長さを c, 他の2辺の長さを a, b とすると、定理はCot (コタンジェント)を変換 三角形の計算 ・ 正三角形 (辺から高さと面積) ・ 正三角形 (高さから辺と面積) ・ 正三角形 (面積から辺と高さ) ・ 直角三角形 (底辺と高さ) ・ 直角三角形 (底辺と斜辺)
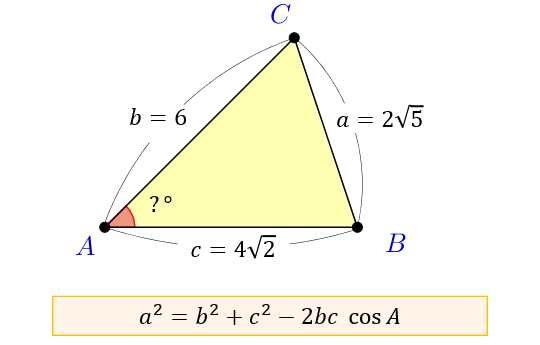
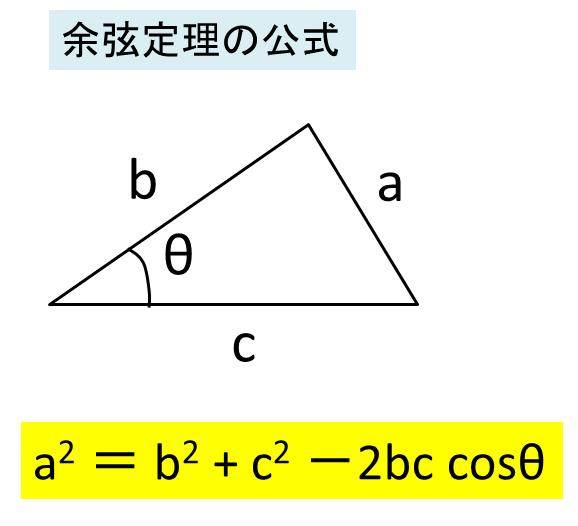
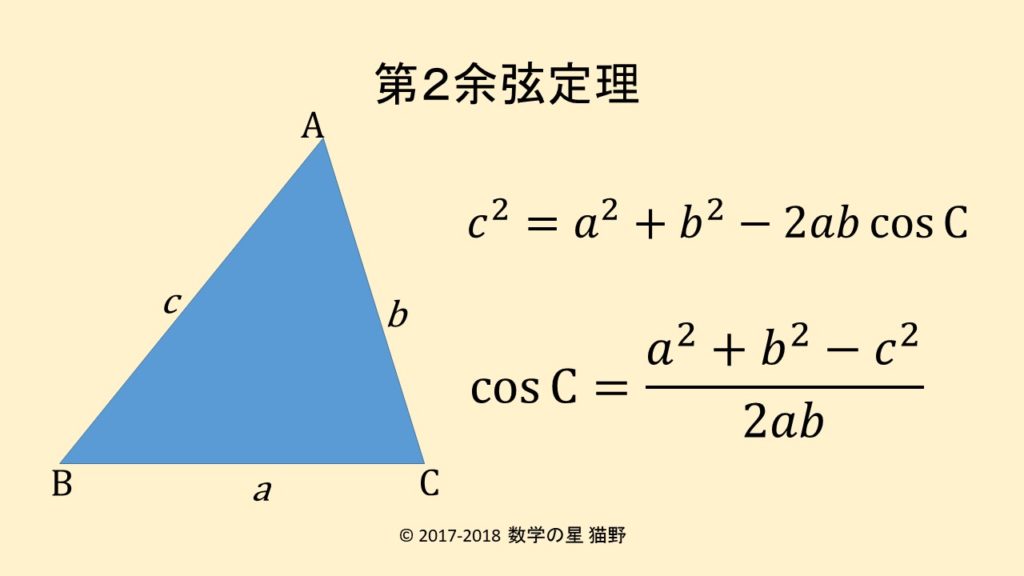
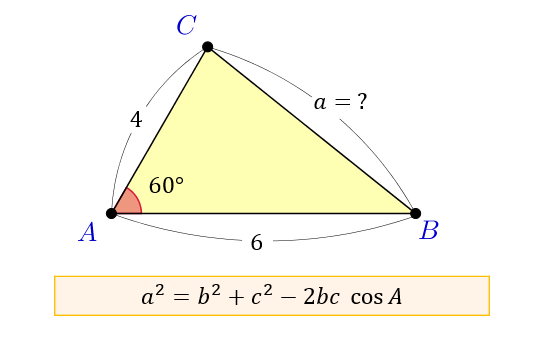
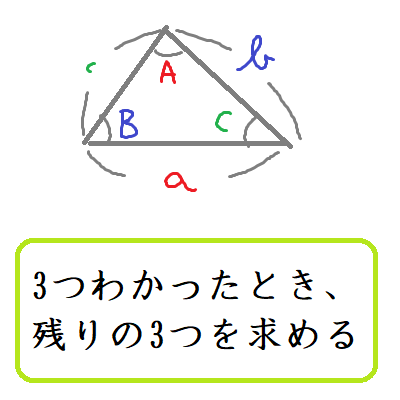
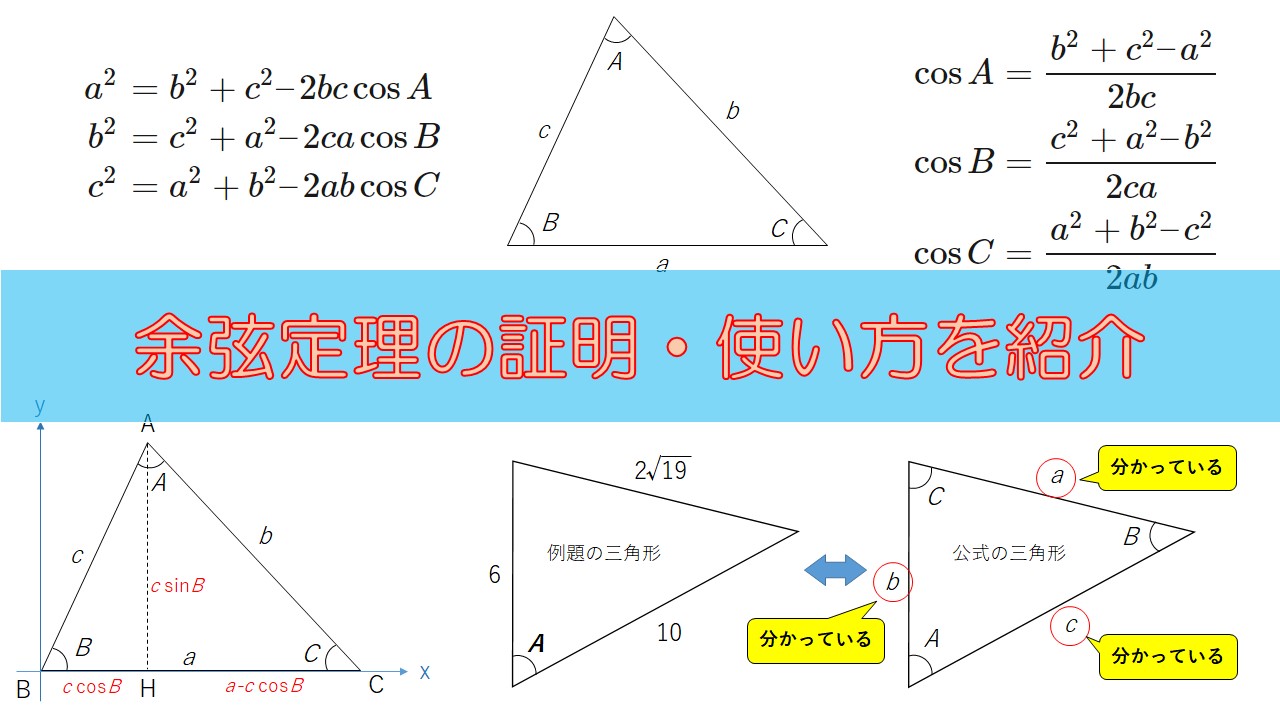
もくじ 1 三平方の定理の内容:直角三角形と辺の長さの関係 11 分からない辺の長さを計算できる三平方の定理;直角三角形において, a^2b^2=c^2 a2 b2 = c2 つまり「斜辺以外の二辺の長さの二乗の和」は「斜辺の二乗」と等しい。 a,b,c a,b,c は直角三角形の3辺の長さで, c c が斜辺です。 詳細は →三平 点 \(C\) の反対側にある線分 \(AB\) の長さを \(c\) とおいたときに、 以下の3つの式が成り立つことを 余弦定理 と言います。 余弦定理は、「2辺の長さとその間の角度」から「残り1辺の
三角形 辺の長さ 定理のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  |  |
 |  | |
 |  |  |
「三角形 辺の長さ 定理」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
「三角形 辺の長さ 定理」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
「三角形 辺の長さ 定理」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
「三角形 辺の長さ 定理」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  | |
「三角形 辺の長さ 定理」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 | ||
「三角形 辺の長さ 定理」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  |  |
 |  |  |
「三角形 辺の長さ 定理」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  |  |
 |  | |
「三角形 辺の長さ 定理」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  | |
「三角形 辺の長さ 定理」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  | |
「三角形 辺の長さ 定理」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「三角形 辺の長さ 定理」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |
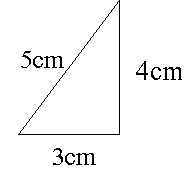
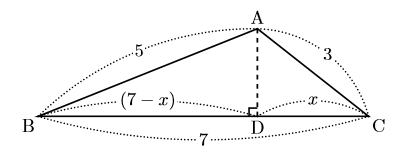
DFの長さをxcmとして、三平方の定理(ピタゴラスの定理)に代入してみると、 13² = 5² x² x = 12 あら不思議! 長さがわからない直角三角形の辺を求めることができたね。 >>三平次のような直角三角形の3辺の長さについては, a 2 b 2 =c 2 が成り立ちます.(これを三平方の定理といいます.) これを用いて3辺の長さのうち2辺の長さが分かっているとき,残りの1辺の長
Incoming Term: 三角形 辺の長さ 定理,




0 件のコメント:
コメントを投稿